7696131553

D. M.§19.da..Gauss.aprze ksztął c e ń e je mentarnych)

Dotyczy liniowych układów dowolnych (układów m równań o u niewiadomych).

Wykorzystuje fakt, że pewne operacje wykonywane na układach równań wprowadzą nas do układu równań, który jest równoważny wyjściowemu układowi równań (równoważne układy równań mają identyczne zbiory rozwiązań). Polega na przekształceniu wyjściowego układu równań liniowych (za pomocą operacji elementarnych - tylko na wierszach) do tzw. postaci kanonicznej (bazowej) i odczytaniu rozwiązania w tej postaci.

^ Metoda Gaussa nie wymaga wcześniejszej weryfikacji zgodności rozwiązywanego układu równali liniowych.

^ Sprzeczność układu w metodzie Gaussa wynika z postaci kanonicznej - wystąpienie sprzecznego równania w postaci kanonicznej.

Chcąc wykorzystać jednocześnie tw. Croneckera-Capellego posługujemy się skróconym zapisem układu równań w postaci macierzy rozszerzonej i wszystkie działania prowadzące do układu równoważnego wykonujemy na tej macierzy.

Eliminujemy z poszczególnych równań kolejne niewiadome, tak by macierz A układu była macierzą jednostkową.

Przykład

fxL + 3x	+ x3 - 9x4 = 10						1 3	1	-ę	1 ^10
2x, + 9x0 + 7x-i — 21 xA =9							2 9	7 -	-21 1 9
				U =	AB =
—Xi — 2x2 + 7x4 = —7							-1 -2	0	7	1 -7
-f 3%2 ^—		Xs - 12x4 = 11					2 3	-1 -	-12 | 11
	1	3 1 -9 | 10			1	3	1 -9	1 10 1		1
	0	3 5-31 -11		1	0	1	1 -2	1 3		•(-3) *
	0	1 1 -2 | 3			0	3	5 -3	1 -U		J
	0	-3 -3 6 | -9			0	-3	-3 6	1	1
	1	0-2-3| 1			1	0 -	-2 -3 |	1		1
	0	1 1 -2 | 3			0	1	1 -2 |	3		1 1
-'V'	0	02 3 | -20		/V 2	0	0	1 L5 |	-10	•c-l) *2
	0	0 0 0 10			0	0	0 0 1	0

(-2) J I

J

I J

1	0	0	^0 1	-19'		1	0	0 1	0	-19'	(
0	1	0	-3,5 |	13		0	1	0 1	3,5	13	-
0	0	1	1,5 |	-10		0	0	1 1	-1,5	-10
0	0	0	^0 1	0		0	0	0 1	0	0	1

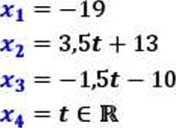
R(U) = R(A) = 3< n=4

układ ma nieskończenie wiele rozwiązań

zależnych od 1 parametru t = x< (tw. Kroneckera-Capellego)

E.    M e t o d a pr z e k s z t ą ł c e ń d o r ó w n o w ą ż n e [ p o s t ą c i k r a m ę r o w s kięj

Każdy niesprzeczny układ równali liniowych A*X = B można przekształcić do odpowiedniej postaci kramerowskiej mającej taki sam zbiór rozwiązań jak wyjściowy układ równań (tzw. równoważna postać kramerowska). Procedura pięcioetapowa:

(1)    Wyznaczyć rząd rozpatrywanego układu liniowego i określić rodzaje rozwiązań

(2)    Wyznaczyć bazę A X = B (układ zredukowany, rdzeń układu) układu równań liniowych złozoną z niektórych równań wyjściowego układu A-X = B (wszystkie równania układu A-X = B są kombinacją liniową równań bazy i mają zbiór rozwiązań = jak układ bazowy).

(3)    Wyznaczyć i ustalić układ niewiadomych bazowych (takich których kolumny współczynników tworzą bazę układu wektorów macierzy A. układu zredukowanego), pozostałe niewiadome nazywamy swobodnymi lub niebazowymi. Liczba niewiadomych bazowych (x„) jest zawsze równa r = R(A). natomiast niewiadomych niebazowych (/„) jest zawsze równa n - R(A).

Maksymalna liczba różnych rozwiązań bazowych wynosi (,,/i po r" - kombinacje).

© Copyright by Ewa Kędzi orczyk    - 78 -    www.matematyka.sosnowiec.pl