8463280649

Zadanie 3. (20 punktów)

3.1. Kostka lodu może ślizgać się bez tarcia po wewnętrznej powierzchni poziomo leżącego walca o promieniu R.

Jej wychylenie z położenia równowagi jest niewielkie w porównaniu z promieniem walca.

Oblicz, jaki będzie okres drgań kostki, jeżeli wychylimy ją z położenia równowagi, a następnie puścimy swobodnie.

3.2. Ciężarek zawieszony na sprężynie wykonuje drgania harmoniczne. Maksymalna prędkość ciężarka wynosi 8 ® . Oblicz prędkość ciężarka w chwili, gdy wychylenie jest równe połowic amplitudy drgań.

Zadanie 4. (20 punktów)

4.1. Metalową kulę o promieniu 10 cm naładowano do potencjału 100V. e₀ = 8.85 • 10 ^l?

a.    oblicz pojemność tej kuli

b.    oblicz ładunek, jaki zgromadził się na kuli.

4.2.    Dwie metalowe kule o promieniach R> i R> połączono przewodzącym drutem i umieszczono daleko od siebie. Układ kul naładowano pewnym ładunkiem. Oblicz, jaki będzie stosunek natężeń pola elektrycznego przy powierzchni kul.

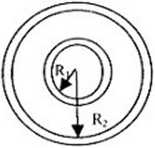
4.3.    Zbudowano kondensator kulisty składający się z dwóch współśrodkowych sfer o promieniach Rj i I<2 (rysunek) wykonanych z przewodnika. Oblicz pojemność tego kondensatora.

Zadanie 5. (20 punktów)

5.1.    Wykaż, że w ruchu elektronu po orbicie kołowej wokół protonu całkowita energia elektronu oraz jego energia kinetyczna spełniają równanie: Hcaikowiu" - Kk.nmcau-

5.2.    Korzystając z pierwszego postulatu Bohra wyprowadź wzór na prędkość elektronu na n-tej orbicie kołowej oraz oblicz prędkość elektronu na pierwszej orbicie.

k = 8,99• 10⁹    ; c = l,6-lO"^,9C: h = 6,63-10'^UJ s; m_e = 9,1 MO"”kg; leV = 1,6- I0‘^,9J

a.    Wyprowadź wzór na energię całkowitą elektronu na n-tej orbicie oraz oblicz (w elektronów oltach) energię całkowitą elektronu na pierwszej orbicie.

b.    Całkowita energia elektronu na orbicie zamkniętej jest ujemna. Wy jaśnij dlaczego. Co stałoby się, gdyby elektronowi dostarczyć takiej energii kinetycznej, że jego całkowita energii byłaby równa zero?