18067 Scan Pic0014

Rozwiązanie zadania 1.5 Prawidłowa odpowiedź: C.

Na ciało o masie m zsuwające się bez tarcia z równi pochyłej działają dwie siły: ciężar mg i siła sprężystości podłoża F_s (patrz[l], str.45). Ich wypadkowa, równoległa do równi siła o wartości

= mg sin a

Rozwiązanie zadania 1.6 Prawidłowa odpowiedź: C.

W fizyce pojęcia „prędkość", „przyspieszenie", ,,siła" itp. to wektory, a więc wielkości posiadające wartość, kierunek i zwrot. Jeśli w zadaniu pytanie dotyczy tylko wartości wektora, powinno to być wyraźnie wyartykułowane. Często jednak zasada ta nie jest przestrzegana. Np. w zadaniu, które rozwiązujemy, będziemy porównywać tylko wartości przyspieszeń, a nie przyspieszenia. Taki brak precyzji językowej pozwala jednak na krótkie i nieskomplikowane sformułowanie tematu, dlatego jest dopuszczalne.

Opierając się na informacjach zawartych w poprzednim zadaniu obliczamy:

h

ai =gsina₁ = gy,

„^2h

«₂ = gsmar₂ = g~j- = 2a_lt

gdzie ar, i a, są kątami nachylenia równi pochyłych do poziomu. Zauważ, że przyspieszenie ciała zsuwającego się z równi nie zależy od masy tego ciała!

Rozwiązanie zadania 1.7 Prawidłowa odpowiedź: C.

Niezależnie od rodzaju ruchu pole powierzchni figury pod wykresem v(t) jest równe drodze przebytej przez ciało.

W rozważanym zadaniu wykresami v(t) są odcinki linii prostej 1 i 2. Z rysunku widzimy, że pole powierzchni pod odcinkiem 2 jest trzykrotnie większe od pola powierzchni pod wykresem 1. Stąd:

Jjfttall

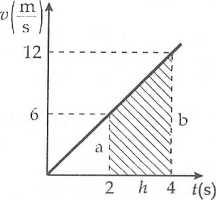
Rozwiązanie zadania 1.8 Prawidłowa odpowiedź: C.

Droga przebyta przez klocek jest równa polu zakreskowanej figury (patrz rozwiązanie poprzedniego zadania). Jest to trapez, którego pole obliczamy następująco:

:$&~(a + b)h = 18 m.

Rozwiązanie zadania 1.9

Prawidłowa odpowiedź: B.

Zakreskowane pole prostokąta wynosi S = aAt. Z definicji przyspieszenia (patrz [1], str. 17) w ruchu prostoliniowym a = -—-.Wielkość S równa jest przyrostowi prędkości Av w tym ruchu.

Rozwiązanie zadania 1.10

Prawidłowa odpowiedź: C.

Droga w ruchu jednostajnie opóźnionym wyraża się wzorem (patrz [1], str. 28):

. 1 *2 S=V₀t~jClt².

Przedstawia on funkcję kwadratową zmiennej t. Dla chwili t = 0 droga s = 0, a więc wykres s(t) musi przechodzić przez początek układu współrzędnych. Ze wzrostem t drugi człon wyrażenia we wzorze rośnie szyb-

- 27 -