41821 Scan Pic0047

rozwiązanie zadnia 3.5 Prawidłowa odpowiedź: D.

Każda z cząstek wytwarza pole centralne, w którym energię potencjalną drugiej cząstki wyrażamy wzorem

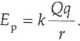
Jeśli ładunki cząstek Qiqsą jednoimienne, wtedy ich iloczyn jest dodatni i dodatnia energia potencjalna maleje ze wzrostem ich wzajemnej odległości r. Jeśli ładunki cząstek Q i 7 są różnoimienne, wtedy ich iloczyn jest ujemny i ujemna energia potencjalna rośnie ze wzrostem ich wzajemnej odległości r (patrz [2], str. 16).

Rozwiązanie zadnia 3.6

Prawidłowa odpowiedź: C.

Potencjał pola wytworzonego przez punktowy ładunek q w odległości r, wyraża się wzorem

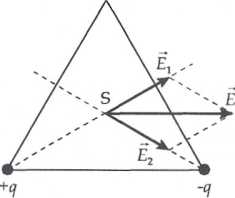
V = k~. r

środek S trójkąta jest równo odległy od obu ładunków. Jeśli więc potencjał w punkcie S ma być równy zeru, to ładunki q^ i q₂ muszą mieć jednakowe wartości i przeciwne znaki. Taki układ ładunków wytwarza w punkcie S pole, którego wektor natężenia E jest równoległy do podstawy trójkąta i zwrócony w prawo lub w lewo. Jest to uzależnione od tego, który z ładunków q₂ i q₂ jest dodatni, a który ujemny.

Rozwiązanie zadnia 3.7 Prawidłowa odpowiedź: D.

Równy zeru potencjał V pola w punkcie P jest sumą potencjałów

y=y₁ + v₂ + v₃ = o,

gdzie V_v V₂ i V₃ to potencjały pól centralnych wytworzonych w punkcie P przez ładunki q_v q₂ i q₃.

Każdy z potencjałów można wyrazić wzorem

V = kQ.

Otrzymujemy więc

_k3±. _{+ k}3l._+k3s- ₌ 0.

2 d

3 d k

po podzieleniu całego równania przez — przyjmuje ono postać:

1.1 _n

ale q₂=2q_v

więc ²‘?i⁺y‘?₃=°/

stąd q₃=-6q_v

Rozwiązanie zadnia 3.8

Prawidłowa odpowiedź: B.

Praca siły zewnętrznej przy przesunięciu ładunku q z A do B wyraża się wzorem:

W₂(a^=?(V,-V_a).

Potencjał V_A w punkcie A jest sumą potencjałów pól wytworzonych w tym punkcie przez ładunki +Q i -Q:

kidtŁ+k®

=-A 21 21

gdzie Q jest wartością bezwzględną ładunku. Podobnie potencjał V_B w punkcie B:

V _=kLQL+_k£Ł

^B 21 l

Podstawiając obliczone potencjały do wzoru na pracę otrzymujemy:

W

^KV2(A-*)

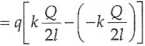
k

JQ

l

Rozwiązanie zadnia 3.9 Prawidłowa odpowiedź: C.

Praca siły zewnętrznej przy przemieszczeniu q z punktu A do B wynosi: gdzie Q jest wartością bezwzględną ładunku.

93 -