Scan Pic0046

Wtedy

stąd

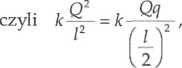
Rozwiązanie zadnia 3.3 Prawidłowa odpowiedź: D.

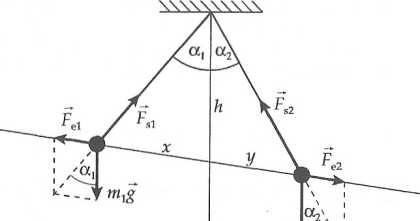
Załóżmy, że kulki mają masy m₁ i m₂ oraz ładunki q_t i q₂. Na każdą z nich będą zatem działać trzy siły: ciężar, siła elektrostatyczna i siła sprężystości nici. Jeśli kulki są oddalone od siebie i pozostają w spoczynku to oznacza to, że:

a)    ładunki i q₂ są jednakowego znaku (kulki odpychają się);

b)    siły działające na każdą kulkę równoważą się.

'

Ponieważ siła sprężystości nici działa wzdłuż kierunku nici, to z twierdzenia b) wynika natychmiast, że dla obu kulek wypadkowa ciężaru i siły elektrycznej ma kierunek nici. A zatem spełnione są następujące proporcje:

h

oraz

m₂g h

Siły elektrostatyczne F_cl i F_c2 są siłami wzajemnego oddziaływania ładunków q_x i q₂ N zasada dynamiki) i niezależnie od tego, czy wartości ładunków są jednakowe, czy też nie, wartości tych sił są sobie równe: & = F_e2. Dzieląc stronami powyższe dwa równania otrzymujemy:

^m2 ₌ y

m₁ x

Lecz z tematu zadania wynika, żex = y, gdyż a_x =    - a, oraz długości

nitek są jednakowe, a więc

m₁ - m₂.

Rozwiązanie zadnia 3.4 Prawidłowa odpowiedź: B.

Każdy z ładunków^ iq₂ wytwarza pole centralne. Aby wektory natężeń E₁ i E₂ tych pól dały w punkcie A w wyniku superpozycji wektor E, muszą mieć zwroty jak na rysunku. Ładunek q_x musi być ujemny, a q₂~ dodatni.

Uwagi do zadań 3.5 - 3.10 Zgodnie z przyjętą umową (patrz [2], str. 15), we wzorze na pracę siły zewnętrznej przy przemieszczaniu ładunku q w centralnym polu elektrostatycznym wytworzonym przez ładunek Q

ładunki należy wstawić razem z ich znakami. r_A jest w tym wzorze początkową odległością q od Q, a r_B - ich odległością końcową.

W konsekwencji, we wzorach

E_p =k^~ i V = fc5. v _r    r

wyrażających energię potencjalną E_p ładunku q w polu wytworzonym przez ładunek Q oraz potencjał V pola wytworzonego przez ładunek Q, ładunki wstawiamy także razem z ich znakami.

91 -