Scan Pic0088

Rozwiązanie zadania 6.7 Prawidłowa odpowiedź: D.

Natężenie prądu w obwodzie fotokomórki zależy od liczby wybitych z fotokatody elektronów, która z kolei zależy od liczby fotonów padających na fotokatodę (patrz [2], str. 109). Liczbę fotonów zwiększymy skupiając światło na fotokatodzie przy pomocy soczewki.

Rozwiązanie zadania 6.8

Prawidłowa odpowiedź: B.

Pole elektryczne wytworzone między katodą i anodą lampy rentgenowskiej wykonuje nad elektronem wysyłanym z katody pracę W = ell nadając mu energię kinetyczną równą tej pracy. Rozpędzony elektron pada na anodę, w której jest hamowany. Tracona w tym procesie energia jest emitowana w postaci różnej liczby kwantów fali elektromagnetycznej (fotonów), których sumaryczna energia nie może jednak przekroczyć energii padającego na anodę elektronu. Jeśli zdarzy się, że podczas hamowania elektronu zostanie wyemitowany tylko jeden foton, jego energia będzie największa z możliwych i równa energii elektronu:

£ = hv_m^ = h—_seU,

^min

gdzie A_min jest krótkofalową granicą widma.

Stąd otrzymujemy:

U= ^V-^ma* = 38-10³ V. e

Rozwiązanie zadania 6.9 Prawidłowa odpowiedź: A.

Zgodnie z informacjami podanymi w rozwiązaniu poprzedniego zadania energia kwantu promieniowania rentgenowskiego o minimalnej długości fali

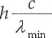
jest równa energii E = ell elektronu padającego na anodę lampy rentgenowskiej, gdzie U jest różnięą potencjałów między katodą i anodą tej lampy:

h—-—*•"== ell,    skąd h =    .

SC    c

Rozwiązanie zadania 6.10 Prawidłowa odpowiedź: D.

Zgodnie z teorią korpuskularno-falową światła (patrz [2], str. 111) energię fotonu wyrażamy wzorem:

E = hv = h—. " 1

Tak więc stosunek energii fotonu promieniowania rentgenowskiego E_x do energii fotonu światła fioletowego E_f wynosi:

Ł ₌ A»440’. E_f A_x

Rozwiązanie zadania 6.11 Prawidłowa odpowiedź: A.

Zgodnie z teorią Einsteina fotonom, podobnie jak cząstkom materialnym, można przypisać masę i pęd. Masę fotonu obliczamy porównując wyrażenie na energię fotonu E = hv ze słynnym wzorem Einsteina dotyczącym równoważności masy i energii: E = mc¹. Z równości

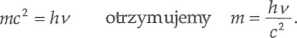
Foton porusza się z szybkością światła c, a zatem jego pęd ma wartość

-_TfTT hv h p = mc = — = — c X

W rozważanym zadaniu

hv E

s

c c

Rozwiązanie zadania 6.12 Prawidłowa odpowiedź: A.

Elektrony o pędzie p mają energię kinetyczną równą

E. m—rno² k 2

1

2

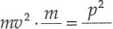
m    2m

Jeśli na skutek hamownia elektronu w anodzie (por. ze wskazówką do zad. 6.8)zostanie wypromieniowany tylko jeden foton, to będzie on miał energię równą energii padającego elektronu

- 175 -