Scan Pic0087

- ROZWIĄZANIA ZADAŃ

Rozwiązanie zadania 6.1 Prawidłowa odpowiedź: C.

W płytce wystąpiło zjawisko fotoelektryczne (patrz [2], str. 106). Fotony promieniowania X padając na płytkę wybiły z niej pewną liczbę elektronów. Zatem płytka metalowa, początkowo obojętna, naładowała się dodatnio.

Rozwiązanie zadania 6.2 Prawidłowa odpowiedź: C.

Jeśli częstotliwość v fotonów jest jednakowa, to oznacza to, że każdy z nich posiada taką samą energię równą

E = h v.

Dzieląc ich łączną energię przez liczbę fotonów otrzymamy energię pojedynczego fotonu. Wynosi ona

380 eV: 190 = 2 eV

i jest większa od pracy wyjścia elektronu z cezu. Każdy z fotonów padając na powierzchnię cezu uwolni jeden elektron, więc liczba uwolnionych elektronów wyniesie 190.

Rozwiązanie zadania 6.3 Prawidłowa odpowiedź: B.

W zjawisku fotoelektrycznym następuje oddziaływanie fotonu z elektronem. Jeden foton może wybić tylko jeden elektron i to w przypadku, gdy energia tego fotonu, E = hv, jest większa od pracy wyjścia W elektronu. Tak więc fotony o energii 1,5 eV nie wybiją żadnego elektronu, natomiast każdy z fotonów o energii 6 eV może wybić jeden elektron. Należy przyjąć, że prawidłowa jest odpowiedź B, chociaż w rzeczywistości tylko około 20% fotonów o energii hv> W wywołuje efekt fotoele-ktryczny (patrz [2], str. 106).

Rozwiązanie zadania 6.4 Prawidłowa odpowiedź: B.

Większe natężenie światła oznacza większą liczbę fotonów padających na katodę fotokomórki. Jeśli założymy, że każdy z fotonów wybija jeden elektron, to im większe natężenie światła padającego, tym większa liczba emitowanych elektronów.

Rozwiązanie zadania 6.5 Prawidłowa odpowiedź: C.

Zgodnie z wzorem Einsteina energia kinetyczna E_k elektronu wybitego z metalu jest równa energii padającego fotonu E = hvpomniejszonej o stałą dla danego metalu pracę W potrzebną do wyrwania elektronu z tego metalu:

E_k = E-W.

Fakt, iż podwojenie energii padającego fotonu powoduje trzykrotny wzrost energii kinetycznej elektronu wybitego z tego samego materiału można zapisać następująco:

3E_k = 2E - W.

Z powyższego ukłądu dwóch równań obliczamy szukaną pracę wyjścia W:

3(E-W) = 2E-W, skąd W

Rozwiązanie zadania 6.6 Prawidłowa odpowiedź: B.

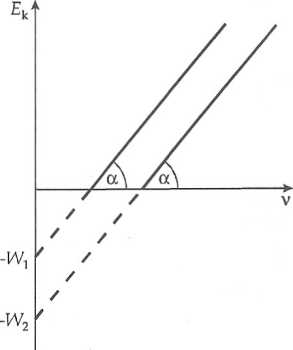
Energia kinetyczna elektronu wybitego z metalu w zjawisku fotoelektrycznym jest liniową funkcją częstotliwości v światła padającego na metal:

E_k = hv-W.

Porównując ten wzór z ogólnym wyrażeniem na funkcję liniową

y = ax + b

widzimy, że stała Plancka h jest równa tangensowi jednakowego dla obu prostych kąta ich nachylenia do osi częstotliwości:

h = a = tg a.

Praca wyjścia, spełniająca we wzorze Einsteina rolę wyrazu wolnego b,

b = - W,

jest różna dla różnych metali.

- 173