23403

Teoria Obwodów - Lekcja 4

4.1. Metoda równań Kirchhoffa

W metodzie tej wykorzystuje się w bezpośredniej formie prawo prądowe i napięciowe Kirchhoffa uzupełnione o równania symboliczne opisujące poszczególne elementy obwodu. W efekcie zastosowania praw Kirchhoffa otrzymuje się układ równań algebraicznych o zespolonych współczynnikach. Jeśli założymy, że obwód posiada b gałęzi i n węzłów to w równaniach opisujących obwód wykorzystuje się (n-1) równań pochodzących z prawa prądowego Kirchhoffa. Pozostałe (b-n+1) równań wynika z prawa napięciowego Kirchhoffa dla (b-n+1) dowolnie wybranych oczek niezależnych (oczka uważa się za niezależne, jeśli równania napięciowe opisujące je są od siebie niezależne) w obwodzie.

Jak z powyższych rozważań wynika w metodzie klasycznej wykorzystującej bezpośrednio prawa Kirchhoffa istnieje potrzeba rozwiązania układu b równań z b niewiadomymi. Jest to więc metoda złożona obliczeniowo, zwłaszcza jeśli weźmie się pod uwagę, że wszystkie równania są zespolona W efekcie metodę tę stosuje się głównie w przypadku obwodów o małej liczbie elementów. Metodę zilustrujemy przykładem liczbowym obliczania prądów i napięć w obwodzie przedstawionym na rys. 4.1.

■ Przykład 4.1

Stosując równania Kirchhoffa należy obliczyć wszystkie prądy i napięcia w obwodzie przedstawionym na rys. 4.1. Przyjąć następujące wartości parametrów obwodu: R ■ 2Q, C=0,5F, L=1H, ff(z) = 1072sin(rtż)V_/ i(t) = 5sin(*ż-45°)A, *>= 1 rad/s.

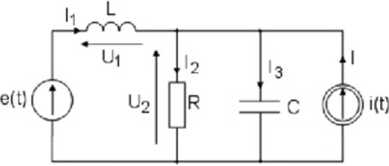
Rys. 4.1 Schemat obwodu do przykładu 4.1 Rozwiązanie

Przy sinusoidalnym wymuszeniu zastosujemy podejście symboliczne, zgodnie z którym przebiegi czasowe są zastąpione wartościami zespolonymi. W przypadku źródeł przyjmuje się:

E- IG**-10, /

TT

Impedancja cewki jest równa Z_L ^mjc<L - j\, a impedancja

■J2

kondensatora Z_c - -j —

(iC

Przy oznaczeniach prądów i napięć jak na rys. 4.1 z praw Kirchhoffa wynikają następujące równania prądowe i napięciowe