24748

Strumieniem wiru nazywa się strumień wektora wiru przechodzący przez powierzchnię A. Elementarny strumień wiru: dqw = W n dA = W cos a dA
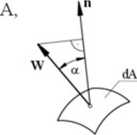
strumień wektora wiru przez tę powierzchnię: qw = \Wn dA
Drugie twierdzenie Helmholtza
Zgodnie z twierdzeniem Gaussa-Ostrogradskiego
Qw
= | Wn dA = J div Jf'dV = J
5W„ 5W <5W,
dx
dy
dz
dV
A V V\
Pochodne cząstkowe współrzędnych Wx, Wy, Wz wektora wiru po x, y, z są następujące
|
swx |
_ d2 v2 |
d2vy |
|
dx |
dy dx |
dzdx |
|
d Wy |
_ 5 2 vx |
d2vz |
|
dy |
dzdy |
dx dy |
|
d W2 |
_d'-vy |
3 2 vx |
|
d z |
dxd z |
dy d z |
Po dodaniu ich stronami otrzymuje się
div(W) =
o
dx dy dz Oznacza to, że m* ustalonym ruchu wirowym dywergencja (rozbieżność linii wirowych) w całym obszarze płynu równa jest zeru, a zatem strumień wiru w cieczy doskonalej zachowuje niezmienna w artość wzdłuż całej długości strugi wirowej. Stanowi to treść drugiego twierdzenia Helmholtza
17
Wyszukiwarka
Podobne podstrony:
f15 Ryc.18. Strumień wektora D przechodzący przez powierzchnię kuli o promieniu r, która otacza doda
Transport ciepła Strumień ciepła AQ /At przechodzący przez powierzchnię A proporcjonalny jest do
układ sił ma wypadkową równą wektorowi głównemu, przechodzącą przez ten punkt przecięcia się
HPIM7978 Sterowaniem nazywa się kierowanie pracą maszyn i urządz przez wpływanie na parametry i prze
HPIM8003 Sterowaniem nazywa się kierowanie pracą maszyn i urząd przez wpływanie na parametry i przeb
81996 skanuj0007 (37) V Azymutem nazywamy kąt <Xab pomiędzy- południkiem przechodzącym przez punk
n ojawił się nam wykres, który przechodzi przez nasze punkty. Można odczytać z wykresu wartość B lub
4 (225) Tarciem nazywa się zjawisko powstawania sit stycznych do powierzchni styku dwóch ciał Tarcie
Statek podczas zmiany przegłębienia przy stałej wyporności obraca się więc wokół osi przechodzącej p
POLSKA POWOJENNA- POLSKA LUBELSKA Polską lubelską nazywa się część ziem polskich wyzwolonych przez A
s gli& 5. WODY PODZIEMNE Wodami podziemnymi nazywa się tu wszystkie rodzaje wody występujące powierz
Zadanie 26 Jak nazywał się zespół śpiewaków, założony w Krakowie przez króla Zygmunta I Starego w 15
Procesy falowe w ośrodkach sprężystych W fizyce falami nazywa się w przestrzeni zaburzeme strumienia
więcej podobnych podstron