26062

Tak zdefiniowany moment wektora względem osi jest skalarem. Definicja ta jest wystarczająca, ponieważ wektor MjfaJe, jest skierowany wzdłuż osi 1, przeto do jego opisu wystarczy podam e tylko jego wartości.

Aby podana na wstępie definicja momentu w^rzględem osi była jednoznaczna, należy wykazać, że rzut na oś 1 momentu wektora a względem punktu O leżącego na tej osi nie zależy od położenia punktu O na tej osi. W tym celu obliczymy moment wektora a względem iimego punktu O' leżącego na osi 1 (rys. 2.12) i dokonamy jego rzutu na tę oś:

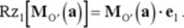
(a)

Na podstawie rys. 2.12 wektor 0'A możemy przedstawić jako sumę w^rektoia O O i r_A :

0'A = 0'0+ r_A .

Po podstawieniu tej zależności do wzoru (a) oraz skorzystaniu z własności iloczynu mieszanego otrzymamy:

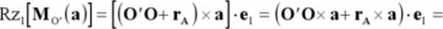
= (0'0x a)-e,+ (r_Ax a)*e, =(e,x 0'0)a+(r_Ax a)-e,.

Ponieważ w-ektoiy e, i O'O są równoległe, ich iloczyn wektorowy jest równy zera: e, x 0'0 = 0. ostatecznie otrzymujemy:

Rz,[M_<y(a)] = (r_A x a)-e, = Rz,[M₀(a)],

czyli rzut na oś momentu wektor a względem punktu na osi rue zależy od połoźema punktu na osi.

Z definicji momentu względem osi wynika, że będzie on równy żeni, jeżeli moment Mo(a) będzie równy zeru lub jego rzut na oś będzie równy zeru Będzie tak, gdy kierunek wektora a będzie przecinał oś 1 lub będzie do niej równoległy.

Z okieślerria momentu wektora względem osi możemy zauważyć, że rzuty momentu Mo(a) wektora a względem początku układu współrzędnych O (rys. 2.11) na osie prostokątnego układu współrzędnych są równocześnie momentami tego wektora względem osi x. y. z. Na podstawie wzorów (2.38) momenty wektora a względem osi x. y. z będą opisane równaniami: