36764

Algorytm realizacji metodą kwantyli

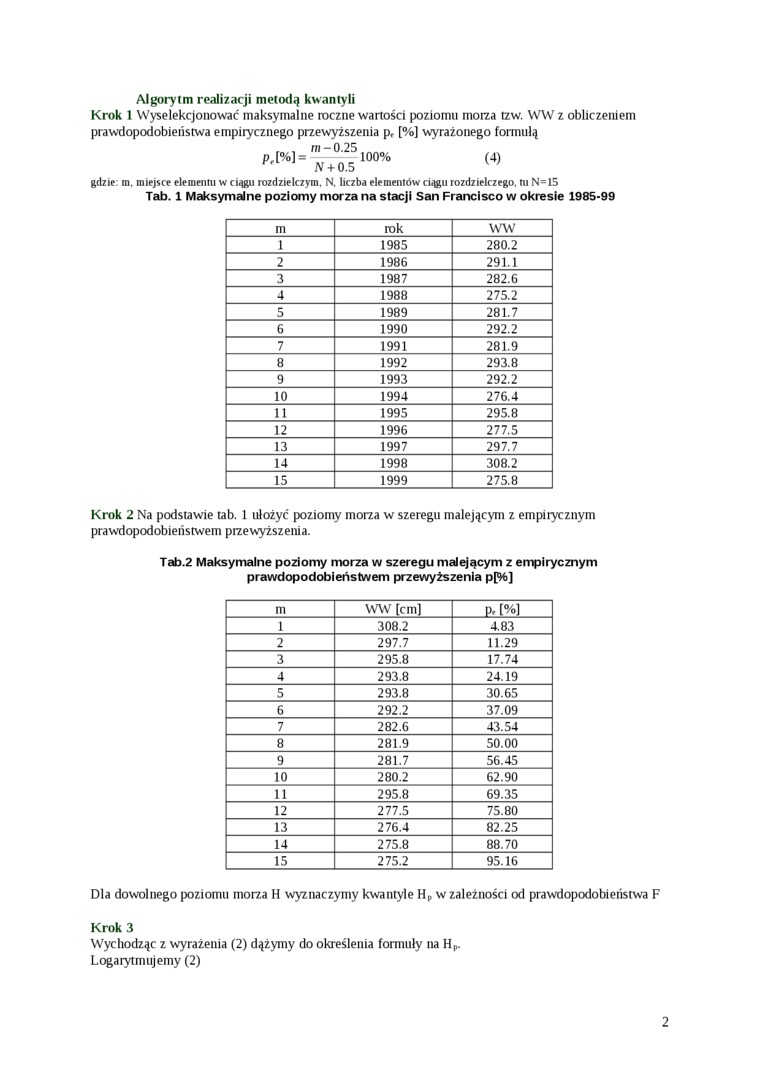
Krok 1 Wyselekcjonować maksymalne roczne wartości poziomu morza tzw. WW z obliczeniem prawdopodobieństwa empirycznego przewyższenia p_f [%] wyrażonego formulą

p,[%l=^m-°'²⁵100%    (4)

JV + 0.5    ¹ J

gdzie m. miejsce elementu w ciągu rozdzielczym. N. liczba elementów ciągu rozdzielczego, tu N=15

Tab. 1 Maksymalne poziomy morza na stacji San Francisco w okresie 1985-99

m	rok	WW
1	1985	280.2
2	1986	291.1
3	1987	282.6
4	1988	275.2
5	1989	281.7
6	1990	292.2
7	1991	281.9
8	1992	293.8
9	1993	292.2
10	1994	276.4
11	1995	295.8
12	1996	277.5
13	1997	297.7
14	1998	308.2
15	1999	275.8

Krok 2 Na podstawie tab. 1 ułożyć poziomy morza w szeregu malejącym z empirycznym prawdopodobieństwem prcewyższenia.

Tab.2 Maksymalne poziomy morza w szeregu malejącym z empirycznym prawdopodobieństwem przewyższenia p[%]

m	WW (cml	P* (%1
1	308.2	4.83
2	297.7	11.29
3	295.8	17.74
4	293.8	24.19
5	293.8	30.65
6	292.2	37.09
7	282.6	43.54
8	281.9	50.00
9	281.7	56.45
10	280.2	62.90
11	295.8	69.35
12	277.5	75.80
13	276.4	82.25
14	275.8	88.70
15	275.2	95.16

Dla dowolnego poziomu morza H wyznaczymy kwantyle H_p w zależności od prawdopodobieństwa F

Krok 3

Wychodząc z wyrażenia (2) dążymy do określenia formuły na H,,. Logarytmujemy (2)

2