116924

Ordinary Least Squares Estimation

*++++**++++++++++*+++++++++++++++++++++++++++++++**++++**++++**+++++*++++++

Dependent variable is Y»

14 observations used for estimation from 1981 to 1994

Regressor	Coefficient	Standard Error	T-Ratiol Prób ]
C	7826.7	3922.0	1.995610.093]
x„	2.5856	1.9624	1.3176(0.236]
x»	32.8297	23.3801	1.4042(0.210]
x3l	-132.0277	1339.2	-0.098589(0.925]
x4,	-61.3255	19.3979	-3.1615(0.020]
Xs,	-0.11933	0.35700	-0.33425(0.750]
x6,	-0.27273	0.34794	-0.78382(0.463]
x7,	0.14844	0.19172	0.77428(0.468]

R-Squared    0.99123 R-Bar-Squared    0.98101

S.E. of Regression    138.4034 F-stat. F 7,6) 96.9325[0.000]

Meanof Dependent Variable 3611.5 S.D. of Dependent Variable 1004.3 Residua! Sum ofSquares 114933.1 DW-statistic    2.2862

****%**************************************************************♦*******

Diagnostic Tests

** * ** * *** *** * *** * * ** * ** * ** *** * * ** ** * ** * * ** * * *** ** * * **** ******* * *** ** *** *** *

*    Test Statistics *    LM Version * F Version *

***************************************************************************

*    A.Serial Correlation*CHSQ(l)=0.65532(0.418]*F(l,5)=0.24554(0.641 J*

*    *    *    *

*    B.Functional Form *CHSQ(1)=0.092187[0.761 ]*F(1,5)=0.033142[0.863]*

*    *    *    *

* C:Nonnality    *CHSQ(2)=0.37048(0.831 ]*    Not applicable *

*    *    *    *

* D:Heteroscedasticity*CHSQ(l)=0.16599[0.684]*F(1,12)=0.14398(0.711]* ***************************************************************************

A:Lagrange multiplier test of residua! serial correlation B:Ramsey's RESET test using the sąuare of the fitted values C:Based on a test of skewness and kurtosis of residuals D.Based on the regression of sąuared residuals on sąuared fitted values

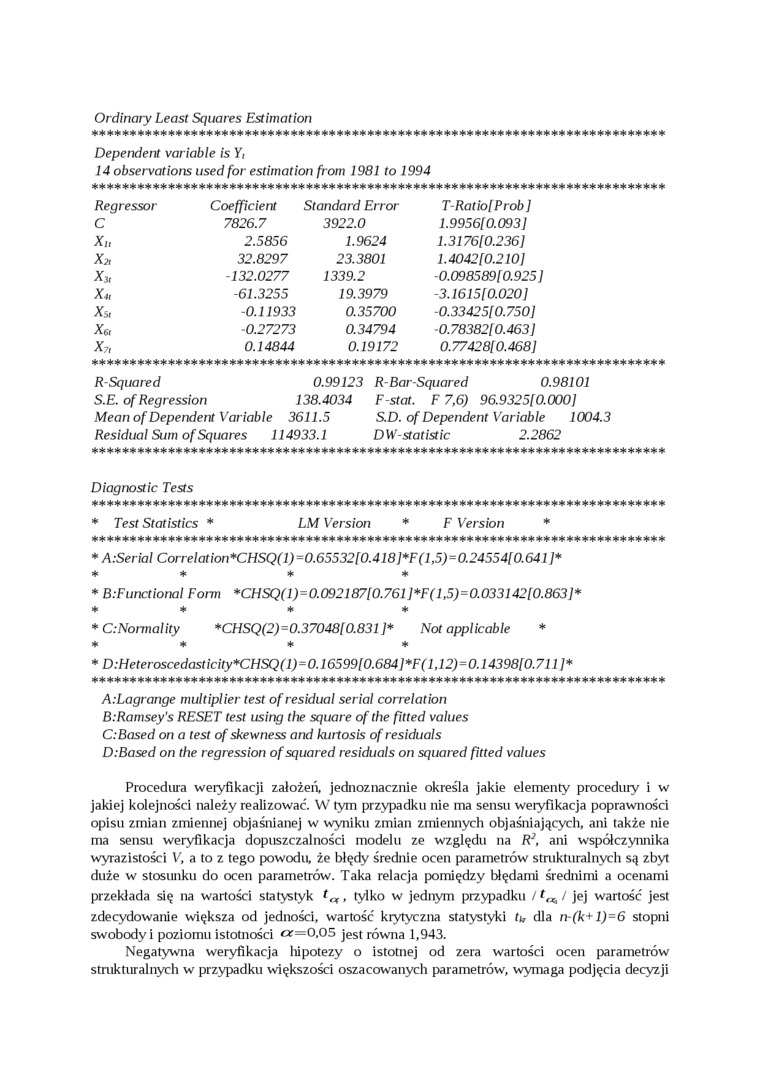
Procedura weryfikacji założeń, jednoznacznie określa jakie elementy procedury i w jakiej kolejności należy realizować. W tym przypadku nie ma sensu weryfikacja poprawności opisu zmian zmiennej objaśnianej w wyniku zmian zmiennych objaśniających, ani także nie ma sensu weryfikacja dopuszczalności modelu ze względu na R³, ani współczynnika wyrazistości V, a to z tego powodu, że błędy średnie ocen parametrów strukturalnych są zbyt duże w stosunku do ocen parametrów. Taka relacja pomiędzy błędami średnimi a ocenami przekłada się na wartości statystyk t_fĄ, tylko w jednym przypadku /    / jej wartość jest

zdecydowanie większa od jedności, wartość krytyczna statystyki ti, dla n-(k+l)=6 stopni swobody i poziomu istotności «=0.05 jest równa 1,943.

Negatywna weryfikacja hipotezy o istotnej od zera wartości ocen parametrów strukturalnych w przypadku większości oszacowanych parametrów, wymaga podjęcia decyzji