123431

Rozkład cechy w całej populacji statystycznej znamy tylko wtedy gdy przeprowadzamy badanie statystyczne pełne, gdy przeprowadzamy badanie statystyczne częściowe to znamy tylko rozkład próby tj. rozkład empiryczny. Rozkład cechy całej zbiorowości statystycznej jest znany nam przy badaniu częściowym to rozkład teoretyczny.

Przykład

Aby zbadać ile czasu tygodniowo przeznacza się w 4 osobowych rodzinach w dużych miastach Polski na prace domowe, wybrano w sposób losowy 1256 takich rodzin i dla tych rodzin wyznaczono średni czas przeznaczony na prace domowe x =10,5 h, odchylenie standardowe s=3,2 h.

Dla tego badania populacje statystyczną generalną to są wszystkie 4 osobowe rodziny dużych miast Polski, jednostką jest każda 4 osobowa rodzina. Cecha którą badamy to czas przeznaczony na prace domowa. Rodzaj cechy jest to cecha mierzalna ciągła.

Rozkład teoretyczny to rozkład zmiennej losowej która przyjmuje wartości równe wykonywania prac domowych we wszystkich tych rodzinach.

Rozkład empiryczny to rozkład tego czasu w zbadanej próbie. Zadaniem statystyki matematycznej jest wnioskowanie o tym co się dzieje we wszystkich rodzinach dużych miast Polski jeśli chodzi o czas poświęcony na prace domowe na podstawi tej liczącej 1256 elementów próby. Zadaniem statystyki matematycznej jest wnioskowanie o rozkładzie teoretycznym na podstawie znajomości rozkładu empirycznego, w ramach wnioskowania empirycznego wyróżnia się dwa zasadnicze działy.

1.    estymacja czyli szacowanie parametrów lub postaci rozkładu teoretycznego na podstawie danych z rozkładu empirycznego

2.    weryfikacja (testowanie) liipotez statystycznych to sprawdzanie określonych przypuszczeń dotyczących typu rozkładu teoretycznego parametrów tego rozkładu, współzależności cech, itp.

Parametry (charakterystyki liczbowe) są to takie liczby np. wartość średnia odchylenie standardowe które w sposób syntetyczny opisują nam zbiorowość statystyczną ze względu na badaną cechę.

Estymacja parametryczna

W teorii estymacji dotyczącej nieznanych parametrów rozkładu teoretycznego wyróżnia się estymację punktową i przedziałową.

Estymacja punktowa polega na znalezieniu takiej liczby która przy z góry założonej dokładności i wynikach uzyskanych z próby może być uznana za najlepszą ocenę nieznanego parametru rozkładu teoretycznego. Estymator Tn nieznanego parametru T w populacji statystycznej nazywamy taką zmienną losową której wartość obliczona na podstawie próby służy do oszacowania nieznanej wartości parametru T. Konkretną wartość liczbową tn=t(xi \2 X3    x„) estymatora Tn obliczono dla wyników (.\i x^ Xj xj) z próby nazywamy

oceną parametru t.

Bardzo ważną rzeczą jest wybór estymatora dla danego parametru. W statystyce określone są własności jakie powinien posiadać ten estymator. Dla najważniejszych parametrów rozkładu teoretycznego przyjmuje się następujące estymatory. Dla wartości przeciętnej średnią

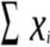
- 1

arytmetyczną z próby ftl X- —

2