Robert Matera data.21.10.2002

Dzień.tyg. środa

WYDZIAŁ INŻYNIERII PRODUKCJI Godzina 11⁰⁰

Kierunek TRiL grupa 2

Ćwiczenie nr. 62

Temat: Wyznaczanie ogniskowych soczewek metodą Bessela i pomiar powierzchni krzywizny soczewek przy użyciu sferometru.

Soczewka sferyczna to substancja załamująca światło, ograniczona dwiema powierzchniami kulistymi o promieniach krzywizny R₁ i R₂.Prostą przechodzącą przez środki krzywizn obu powierzchni nazywamy osią główną soczewki.

Ognisko główne soczewki skupiającej stanowi punkt, w którym przecinają się po załamaniu w soczewce promienie równoległe do głównej osi optycznej. W ognisku głównym soczewki rozpraszającej przecinają się przedłużenia promieni załamanych w soczewce, padających na nią równolegle do osi głównej. Odległość ogniska od środka soczewki nazywamy ogniskową soczewki i oznaczamy literą ƒ.

Ogniskowa soczewki zależy od współczynnika załamania materiału, z którego jest soczewka wykonana oraz od jej promieni krzywizn R₁ i R₂. W przypadku

Soczewek cienkich ogniskową możemy obliczyć ze wzoru:

=(n-1)(
)

Promień krzywizny wypukłej jest dodatni, a powierzchni wklęsłej jest ujemny.

Wielkość D =1/ƒ nazywamy zdolnością zbierającą soczewki.

Jednostką zdolności zbierającej jest dioptria [D] 1D=1/m .

Wyznaczanie ogniskowej soczewki skupiającej i rozpraszającej metodą Bessela.

Odległości a i b (przedmiotu i obrazu od soczewki) są zmienne, tzn. przy stałej odległości l przedmiotu od ekranu istnieją dwie pozycje soczewki, przy której na ekranie otrzymujemy ostry obraz: raz - powiększony, drugi raz pomniejszony. Obie sytuacje różnią się między sobą, tym że odległość a i b zmieniają się rolami. Zgodnie z oznaczeniami: a = b' , b = a', czyli :

a + b = l i a - b = d .

Wyznaczone w ten sposób odległości a i b podstawiamy do równania soczewek:

Otrzymujemy wówczas następujący wzór na ogniskową ƒ.

ƒ=

Ponieważ soczewki rozpraszające nie dają obrazów rzeczywistych, łączymy soczewkę rozpraszającą z soczewką skupiającą w układ soczewek. Przekształcając wzór 1/ƒ_u=1/ƒ₁+1/ƒ₂ otrzymujemy:

ƒ₂=(ƒ_1*ƒ_u) : ƒ₁-ƒ_u

Wyznaczanie promienia krzywizny soczewek przy udziale sferometru .

Wysokość h czasy kulistej możemy zmierzyć za pomocą sferometru. Zasadniczym elementem pomiarowym sferometru jest ruchoma, pionowa śruba mikrometryczna o dokładności 0.01 mm.

Promień R krzywizny soczewki, promień podstawy r czaszy kulistej i wysokość h czaszy spełniają związek:

r²= (2R-h)h

Okrąg stanowiący podstawę czaszy kulistej jest okręgiem opisanym na trójkącie równobocznym o boku c , utworzonym przez podstawę sferometru. Zachodzi związek:

r = c/
, który po podstawieniu do w/w wzoru na promień krzywizny :

R = c²/6h + h/2

Zatem mierząc c i h możemy wyznaczyć promień krzywizny. Wysokość czasy kulistej jest różnicą między wskazaniem sferometru ustawionego na powierzchni płaskiej i wskazaniem po ustawieniu sferometru na jednej z powierzchni badanej soczewki.

Współczynnik załamania materiału obliczamy :

n = R₁R₂ / ƒ( R₁ +R₂) + 1

Wykonanie ćwiczenia:

1. Odczytujemy na ławie optycznej odległość l przedmiotu od ekranu.

l = 0,80 m

2. Szukamy takiego położenia b₁ soczewki, przy którym na ekranie otrzymujemy ostry obraz powiększony, a następnie położenia b₂ odpowiadającego obrazowi zmniejszonemu.

Obraz powiększony: b₁ = 0,765 m

= 0,763 m średnia b₁= (0,765+0,763+0,764)/3

= 0,764 m =0,764 m

Obraz zmniejszony: b₂ = 0,174 m

= 0,175 m średnia b₂= (0,174+0,175+0,173)/3 = 0,173 m = 0,174 m

Różnica odległości obrazów od soczewki d =
= 0,59 m

ƒ₁ = (0,9)²-(0,59)² / 4_* 0,9 = 0,128 m

Dla układu soczewek :

Obraz powiększony b₁ = 0,668 m

= 0,669 m średnia b₁ = (0,668+0,669+0,670)/3

= 0,670 m = 0,669 m

Obraz zmniejszony b₂ = 0,291 m

= 0,290 m średnia b₂ = (0,291+0,290+0,292)/3

= 0,292 m = 0,291 m

d =
= 0,378 m

ƒ_u = 0,185 m

zatem ogniskowa soczewki rozpraszającej po podstawieniu do wzoru wynosi: ƒ₂ = (0,128*0,185)/(0,128-0,185) = -0,415 m

Wyznaczanie promieni krzywizn soczewek.

1.Na kartce papieru odciskamy ślady nóżek podstawki sferometru. Przykładamy ostrza suwmiarki do zaznaczonych na papierze śladów i odczytujemy kolejno długości trzech boków trójkąta. Średnią otrzymanych wyników przyjmujemy jako wartość boku trójkąta równobocznego - c.

c₁₌0,025 m

c₂=0,0252 m średnia c = (0,025+0,0252+0,0251)/3

c₃=0,0251 m =0,0251 m

2. ustalamy położenie zerowe sferometru - ustawiamy sferometr na gładkiej płytce szklanej i odczytujemy wskazanie :

h=0,00014 m

h=0,00013 m średnia h₀= (0,00014+0,00013+0,00015)/3

h=0,00015 m =0,00014 m

3. Ustawiamy sferometr na powierzchni wypukłej soczewki skupiającej i odczytujemy wartość h₁. Różnica h= h₁-h₀ jest wysokością czasy odciętej danej soczewki.

h₁ = 0,0025 m

h₁ = 0,0024 m średnia h₁=(0,0025+0,0024+0,0026)/3

h₁ = 0,0026 m = 0,0025 m

h= h₁-h₀ h = 0,00236 m

R = c²/6h + h/2

zatem promień krzywizny R₁ = 0,0000063/0,0142 + 0,00236/2 = 0,1796

Dla powierzchni wklęsłej

h₂=0,00026 m

h₂=0,00025 m średnia h₂=( 0,00026+0,00025+0,00024)/3

h₂=0,00024 m = 0,00025 m

h=h₂-h₀ h= 0,00011 m

zatem R₂ = 0,0000063/0,00066+0,00011/2 = 0,001 m

Dla soczewki rozpraszającej:

h₁=0,00092 m

h₁=0,00093 m średnia h₁=(0,00092+0,00093+0,00091)/3

h₁=0,00091 m =0,00092 m

h=h₁-h₀ h=0,00078 m

R₁= 0,0000063/0,0047+0,00078/2 = 0,0017 m

h₂=0,0016 m

h₂=0,0017 m średnie h₂=(0,0016+0,0017+0,0018)/3

h₂=0,0018 m =0,0017 m

h=h₂-h₀ h=0,0016 m

R_{2 =} 0,0000063/0,0094+0,0016/2 = 0,0015 m

Przystępuję do obliczania współczynnika załamania światła:

n = R₁R₂ / ƒ( R₁ +R₂) + 1

dla soczewki skupiającej:

n₁= R₁R₂ / ƒ( R₁ +R₂) + 1 = (0,1796*0,001)/0,128(0,1796+0,001)+1 = 0,0001796/0,0231168+1= 1,008

dla soczewki rozpraszającej:

n₂= R₁R₂ / ƒ( R₁ +R₂) + 1 =(0,0017*0,0015)/0,185(0,0017+0,0015)+1 = 0,00000255/0,231168 + 1 = 1,0001

Rachunek błędów:

Δl= Δd=0,002 m

Błąd pomiaru ogniskowej:

Δƒ=(l+ d)²Δl/4l²

Soczewka skupiająca

Δƒ₁=(0,9+0,59)²*0,002 /3,6² = 0,00034

Układ soczewek

Δƒ₂=(0,9+0,378)²*0,002 /3,6² = 0,00025

Błąd pomiaru krzywizny:

ΔR=

+
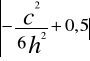
Δh

Δc₁=0,00251-0,00250 + 0,0001=0,00011 m

Δc₂=0,00251-0,00251 + 0,0001=0,0001 m

Δc₃=0,00251-0,00252 + 0,0001=0,00009 m

Δc=0,0001 m

Δh=0,00002 m

Dla soczewki skupiającej:

ΔR₁ = 0,0251/0,00708•0,0001+ -0,81/0,0000334+0,5•0,00002 =

= 0,000036+ 0,485 = 0,485

ΔR₂=0,0251/0,00033•0,0001+-0,81/0,000072+0,5•0,00002 =

= 0,0076 + 0,225 = 0,2326

Dla układu soczewek

ΔR₁ = 0,0251/0,00234•0,0001+ -0,81/0,00000365+0,5•0,00002 =

= 0,0076+ 4,43 = 4,44

ΔR₂=0,0251/0,0048•0,0001+-0,81/0,000016+0,5•0,00002 =

= 0,00052 + 1,0125 = 1,013

Błąd Δn :

Δn=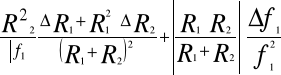

Δn₁=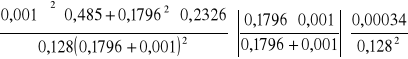
=1,797*0,000995*0,02≈0,0000358

Δn₂=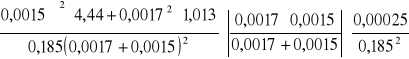
=6,8188*7,968*0,0073=0,3966

Wnioski :

Wyznaczając ogniskową soczewki metodą Bessela dowiedzieliśmy się, że istnieją dwa położenia soczewki między obrazem a ekranem dające ostry obraz. Pomiary dokonywane tą metodą wydają się być w miarę dokładne ponieważ pozwalają ustalić ogniskową bez wyznaczania dokładnego położenia środka optycznego soczewki. Do wyznaczenia ogniskowej soczewki rozpraszającej trzeba połączyć soczewkę rozp. w układ z soczewką zbierającą ponieważ soczewka rozpraszająca daje tylko obraz pozorny. Przy wyznaczanie promienia krzywizny jedynym problemem pozostaje tylko prawidłowe odczytanie wskazania sferometru.

---