Politechnika Krakowska |
|
rok: 1998/99 |
nr. ćwiczenia |
Fizyka Techniczna |
MARCIN |
semestr: I |
4 A |
Grupa: C |
KUK |
Ocena: |
Podpis: |
Zespół: 8 |
|
|
|
Wyznaczanie przyspieszenia ziemskiego metodą wahadła matematycznego.
Wprowadzenie teoretyczne.
Wyprowadzenie wzoru na okres drgań wahadła matematycznego.
Wykonanie pomiarów oraz obliczeń potrzebnych do doświadczenia.
Obliczanie przyspieszenia.
Wniosek.
Wprowadzenie teoretyczne.
Przyśpieszenie ziemskie - przyśpieszenie ciał swobodnie spadających na ziemię pod wpływem działania siły przyciągania grawitacyjnego. Wartość przyspieszenia ziemskiego jest stała dla wszystkich ciał w danym punkcie ziemi , a zależy od wysokości nad poziomem morza, szerokości geograficznej lokalnego rozkładu mas wewnątrz ziemi i innych.
Do pomiaru przyspieszenia ziemskiego używamy wahadła matematycznego.
Wahadło matematyczne - punkt materialny, zawieszony na nieważkiej i nierozciągliwej nici. Realizujemy je zawieszając ciężarek na cienkim drucie, przy czym rozmiary ciężarka muszą być małe w stosunku do długości drutu (rys. 1).
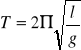
Wahadło, wychylone o mały kąt z położenia równowagi, wykonuje ruch drgający prosty o okresie wahań:
gdzie:
l - długość wahadła, tj. odległość środka ciężkości ciała zawieszonego od osi obrotu
g - przyspieszenie ziemskie
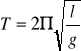
![]()
stąd:
![]()
Ruch harmoniczny - (ruch drgający prosty) ruch, w którym współrzędne określające położenie punktu są opisane funkcjami trygonometrycznymi sinus lub cosinus, przyspieszenie jest proporcjonalne do wychylenia, przy czym współczynnik proporcjonalności jest ujemny.
Maksymalne przyspieszenie ruchu harmonicznego wyrażone jest wzorem:
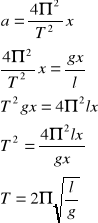
Okres wahań wahadła matematycznego zależy od długości nici oraz od wartości działającego w danym miejscu przyspieszenia ziemskiego. Na okres nie ma natomiast wpływu amplituda i masa wahadła.
Wyprowadzenie wzoru na okres drgań wahadła matematycznego.
Siła ciężkości działająca na wahadło jest wypadkową stycznej do toru a normalną:![]()
![]()
![]()
z podobieństwa trójkąta otrzymuję:
![]()
stąd:
![]()
podstawiając otrzymuję:
![]()
wiedząc, że:
![]()
oraz:
![]()
podstawiając te dwie zależności otrzymuję:
![]()
![]()
stąd:
![]()
przyspieszenie jest równe:
![]()
więc:
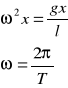
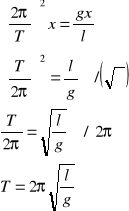
po przekształceniu uzyskujemy:
![]()
gdzie:
![]()
- siła ciężkości
![]()
- styczna do toru
![]()
- normalna
![]()
- wychylenie
![]()
- długość wahadła
![]()
- masa
![]()
- przyspieszenie ziemskie
![]()
- przyspieszenie
Ponieważ długość wahadła oraz przyspieszenie ziemskie jest stałe to siła wprawiająca w ruch wahadło matematyczne jest wprost proporcjonalna do wychylenia.
Wykonanie pomiarów oraz obliczeń potrzebnych do doświadczenia
Długość wahadła
Długość wahadła matematycznego jest równa:
![]()
gdzie:
![]()
- długość nici
![]()
- średnica kulki
Pomiar nici wahadła matematycznego
Niepewność systematyczna: ![]()
Seria próbna:
|
|
|
|
1 |
111,00 |
-0,25 |
0,06 |
2 |
111,40 |
0,15 |
0,02 |
3 |
111,20 |
-0,05 |
0,00 |
4 |
111,40 |
0,15 |
0,02 |
SUMA |
445,00 |
0,00 |
0,11 |
![]()
Średni błąd kwadratowy:
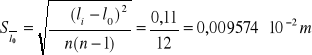
![]()
Liczba pomiarów jest mniejsza od 10, dlatego należy nanieść poprawkę Studenta - Fishera:
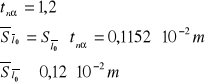
Błąd maksymalny:
![]()
Długość nici
Z błędem maksymalnym:
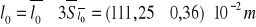
Z błędem standardowym:
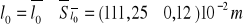
Pomiar średnicy kulki
Niepewność systematyczna: ![]()
Seria próbna:
|
|
|
|
1 |
1,90 |
0,04167 |
0,00174 |
2 |
1,80 |
-0,0583 |
0,0034 |
3 |
1,87 |
0,01167 |
0,00014 |
4 |
1,87 |
0,01167 |
0,00014 |
5 |
1,84 |
-0,0183 |
0,00034 |
6 |
1,87 |
0,01167 |
0,00014 |
SUMA |
11,15 |
|
0,00588 |
![]()
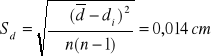
Średnica kulki: ![]()
Promień kulki
Z błędem maksymalnym:
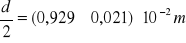
Z błędem standardowym:
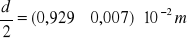
Długość wahadła
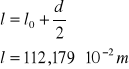
Błąd maksymalny:
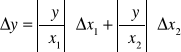
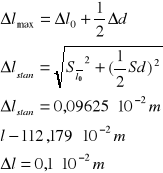
Błąd średni kwadratowy:
![]()
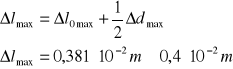
Błąd maksymalny:
![]()
Pomiar okresu T
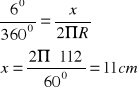
Seria próbna:
|
|
|
|
1 |
21,18 |
0,754 |
0,56852 |
2 |
19,50 |
-0,926 |
0,85748 |
3 |
19,15 |
-1,276 |
1,62818 |
4 |
20,94 |
0,514 |
0,2642 |
5 |
21,17 |
0,744 |
0,55354 |
6 |
20,97 |
0,544 |
0,29594 |
7 |
20,78 |
0,354 |
0,12532 |
8 |
21,06 |
0,634 |
0,40196 |
9 |
18,40 |
-2,026 |
4,10468 |
10 |
21,11 |
0,684 |
0,46786 |
SUMA |
204,26 |
|
9,26764 |
![]()
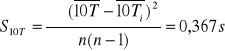
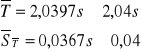
Okres T wynosi
Z błędem maksymalnym:
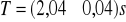
Z błędem standardowym:
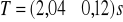
Obliczanie przyspieszenia
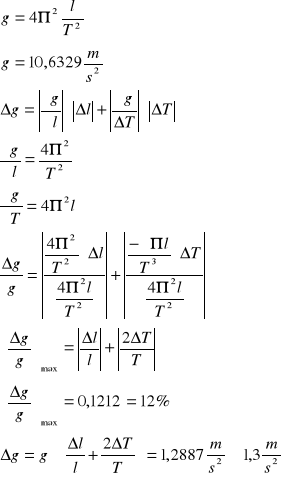
Doświadczalne przyspieszenie ziemskie wynosi:
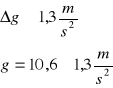
Przyspieszenie ziemskie dla Krakowa zdefiniowane w tablicach wynosi:
![]()
Kryterium zgodności: ![]()
Wniosek
Wyznaczone doświadczalnie przyspieszenie ziemskie wyniosło ![]()
.
Tablicowe przyspieszenie dla Krakowa wynosi ![]()
. Wartość wyznaczona zawiera się w dopuszczalnej granicy błędu. Na niedokładność pomiaru miała wpływ niedoskonałość ludzkich zmysłów oraz mało precyzyjne narzędzia miernicze używane przez prowadzących doświadczenie. Dodtkowym czynnikiem zakrzywiającym wynik pomiaru był brak uwzględnienia pod uwagę oporu powietrza itp.
7
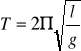
![]()
Wyszukiwarka
Podobne podstrony:
ćw.4, 11, Politechnika Krakowska
ćw.40, 40 Bernady, Politechnika Krakowska
ćw.21, 21, Politechnika Krakowska
ćw.5, 05 Gorski, Politechnika Krakowska
ćw.19, 19 Karczewski, Politechnika Krakowska
ćw.19, 19 Karczewski, Politechnika Krakowska
ćw.19, 19 Bernady, Politechnika Krakowska
ćw.17, 25 Karczewski, Politechnika Krakowska
Konspekt do cw. lab.-termowizja, Energetyka Politechnika Krakowska Wydział Mechaniczny I stopień, Mi
ćw.39, 39 Gorski 2, Politechnika Krakowska
ćw.40, 40 Balawender, Politechnika Krakowska
Fizyka cw 1, Politechnika Krakowska BUDOWNICTWO, I ROK, Fizyka
ćw.34, opracowanie34, Politechnika Krakowska
ćw.33, 33 Bernady 2, Politechnika Krakowska
ćw.40, 40 Karczewski, Politechnika Krakowska
ćw.2, Pomiar lepkości cieczy, Politechnika Krakowska
ćw.27, 27, Politechnika Krakowska
ćw.19, 19 Gorski 3, Politechnika Krakowska
ćw.19, 19 Gorski 2, Politechnika Krakowska
więcej podobnych podstron