Uproszczenie procesu tworzenia portfela

- modele wskaźnikowe

Wprowadzone do teorii portfelowej innowacje można podzielić na dwie kategorie:

1. zmniejszono liczbę danych niezbędnych do rozwiązania zadania wyboru portfela i uproszczono ich strukturę,

2. uproszczono metody obliczeń przeprowadzanych przy wyznaczaniu optymalnego portfela.

Teoria portfela Markowitza ma istotną wadę - dużą złożoność obliczeniową.

Aby zestawić według procedury Markowitza portfel składający się z N akcji należy:

1. oszacować N stóp zwrotu,

2. oszacować N wariancji stóp zwrotu,

3. obliczyć współczynniki korelacji pomiędzy każdą parą akcji wchodzących w skład portfela - takich współczynników jest N(N-1)/2.

Sposobem, który umożliwia znaczne uproszczenie procesu tworzenia portfeli efektywnych są tzw. modele wskaźnikowe.

Cechą tych modeli są znacznie mniejsze - w porównaniu z metodą Markowitza - wymagania co do ilości informacji niezbędnych do ich zastosowania.

W praktyce wyróżnia się modele jedno- i wielowskaźnikowe.

Model jednowskaźnikowy

Model jednowskaźnikowy, będący uproszczoną wersją metody Markowitza, opracował William Sharpe (artykuł „A Simplified Model of Portfolio Analysis” opublikowany w 1963 r.).

W modelu Sharpe'a stopa zwrotu waloru uzależniona jest od działania jednego czynnika, który można określić jako czynnik rynku (giełdy).

Konstrukcja modelu jednowskaźnikowego opiera się na dwóch podstawowych założeniach:

1. stopy zwrotu poszczególnych akcji zależą od określonego wskaźnika, charakteryzującego cały rynek akcji (najczęściej do tego celu używa się szerokiego wskaźnika giełdowego, np. S&P 500 czy WIG). Oznacza to, że jedyną przyczyną zmienności stóp zwrotu poszczególnych akcji jest zmienność stopy zwrotu wskaźnika rynkowego.

2. zmienność stóp zwrotu z poszczególnych akcji w kolejnych okresach zależy od dwóch rodzajów czynników:

1. makroekonomicznych - oddziałujących na całą gospodarkę,

2. mikroekonomicznych - oddziałujących tylko na poszczególne firmy.

Podstawowe równanie modelu jednowskaźnikowego można zapisać następująco:

gdzie:

stopa zwrotu z akcji lub portfela w okresie t,

wyraz wolny równania regresji,

współczynnik kierunkowy równania regresji,

stopa zwrotu wskaźnika rynkowego w

okresie t,

składnik resztowy (losowy) równania regresji.

Model Sharpe'a jest modelem liniowej zależności stopy zwrotu akcji (lub portfela) od stopy zwrotu wskaźnika rynkowego.

Jest to zależność przybliżona, ponieważ w modelu występuje składnik losowy (resztowy).

Ważną rolę w modelu odgrywa współczynnik kierunkowy prostej, zwany współczynnikiem beta.

Współczynnik beta wskazuje, o ile zmieni się (w przybliżeniu) stopa zwrotu akcji, jeżeli stopa zwrotu wskaźnika rynku zmieni się o jeden procent.

Inaczej mówiąc, współczynnik beta określa stopień wrażliwości danej akcji na zmiany stopy zwrotu wskaźnika rynku.

Wyraz wolny interpretujemy jako stopę zwrotu z danej akcji (lub portfela), w przypadku gdy stopa zwrotu wskaźnika rynkowego wynosi zero.

W modelu jednowskaźnikowym kowariancję między stopami zwrotu dwóch akcji można wyrazić za pomocą następującego wzoru:

gdzie:

- współczynniki beta rozpatrywanych akcji, określające stopień reakcji tych akcji na zmiany zachodzące na rynku,

σ²(r_M) - wariancja stopy zwrotu wskaźnika rynkowego.

Na podstawie modelu jednowskaźnikowego wariancję stopy zwrotu akcji lub portfela możemy wyznaczyć w następujący (uproszczony) sposób:

=
+

Po prawej stronie równania występują dwa składniki:

• pierwszy składnik zwany jest ryzykiem systematycznym;

• drugi składnik to wariancja resztowa, reprezentująca ryzyko niesystematyczne.

Równanie na obliczenie wariancji ma zastosowanie zarówno do pojedynczych akcji, jak i do portfeli składających się z wielu akcji.

W odniesieniu do portfela przyjmuje ono następującą postać:

=
+

Współczynnik beta portfela jest średnią ważoną współczynników beta akcji wchodzących w skład tego portfela:

Model jednowskaźnikowy zakłada, że składniki resztowe nie są ze sobą skorelowane. Z założenia tego wynika, że kowariancje pomiędzy składnikami resztowymi każdej pary akcji są równe zeru.

Wariancję resztową portfela możemy obliczyć za pomocą następującego wzoru:

Jeżeli, zgodnie z założeniami modelu jednowskaźnikowego, składniki resztowe poszczególnych akcji nie są ze sobą skorelowane, to wraz ze wzrostem liczby akcji w portfelu wariancja resztowa portfela będzie zmierzać do zera.

Ostatecznie, po podstawieniu odpowiednich wyrażeń, wzór na wariancję (ryzyko) portfela w modelu jednowskaźnikowym możemy zapisać następująco:

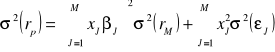
Pierwszy składnik sumy z prawej strony równania odzwierciedla ryzyko systematyczne portfela, natomiast drugi - ryzyko niesystematyczne (wariancję resztową) portfela.

Stosując model jednowskaźnikowy, osiągnęliśmy zakładany cel, tzn. zmniejszenie liczby obliczeń niezbędnych do wyznaczenia wariancji portfela.

Na przykład dla portfela składającego się z akcji 150 firm:

1. przy zastosowaniu procedury Markowitza zachodzi konieczność obliczenia 11 175 (N(N-1)/2) samych tylko współczynników korelacji;

2. w modelu jednowskaźnikowym konieczne jest obliczenie 150 współczynników beta dla poszczególnych akcji, 150 wariancji resztowych oraz jednej wariancji wskaźnika rynkowego, czyli łącznie 301 parametrów.

Przykład

Dekompozycja stóp zwrotu w modelu jednowskaźnikowym.

Złożenia:

1. Stopy zwrotu z akcji J i wskaźnika rynkowego kształtują się jak w tabeli (dane w %).

2. Współczynnik beta akcji J wynosi 1,5.

Okres


=
+
+

1 10 4 10 = + +

2 3 2 3 = + -

3 15 8 15 = + +

4 9 6 9 = + -

5 3 0 3 = + +

40 20 40 =

Oczekiwaną (średnią) stopę zwrotu - wykorzystując model jednowskaźnikowy - można obliczyć następująco:

= 10/5 = 2

= 20/5 = 4

= 2 + 1,5 × 4 = 8

Na podstawie danych z tabeli średnia stopa zwrotu również wynosi 8 (40/5=8).

Z kolei wariancja stopy zwrotu równa jest:

=

+

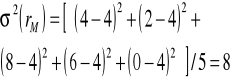
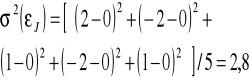
Szacowanie współczynników beta i
.

W przedstawionym przykładzie liczbowym jeden z parametrów (współczynnik β) wzięty był z zewnątrz.

Można postawić pytanie, jak obliczyć współczynniki beta dla poszczególnych akcji?

Najczęściej stosowaną metodą jest obliczanie współczynników beta na podstawie danych z przeszłości. Przyjmuje się w tym przypadku założenie, że współczynniki beta są stabilne w czasie.

W celu oszacowania współczynnika beta danej spółki w oparciu o dane z przeszłości można posłużyć się następującym wzorem:

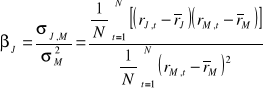
gdzie:

σ_J,M - kowariancja pomiędzy stopą zwrotu akcji J i rynku.

Z kolei współczynniki
można oszacować za pomocą następującego wzoru:

Wykorzystując dane z poprzedniego przykładu można obliczyć zarówno współczynnik
, jak i współczynnik
.

Okres
x
= wartość

1 (10 - 8) x (4 - 4) = 0

2 (3 - 8) x (2 - 4) = 10

3 (15 - 8) x (8 - 4) = 28

4 (9 - 8) x (6 - 4) = 2

5 (3 - 8) x (0 - 4) = 20

Suma 60

Kowariancja pomiędzy stopą zwrotu akcji J i rynkiem wynosi w tym przykładzie 60/5 = 12.

Z kolei wariancja rynkowej stopy zwrotu to przeciętna wartość sumy kwadratów odchyleń od średniej, czyli suma (
)² dzielona przez 5, co daje 40/5 = 8.

A zatem:

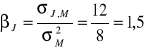
natomiast:

Modele wielowskaźnikowe

Modele wielowskaźnikowe opierają się na założeniu, że korelacje stóp zwrotu poszczególnych akcji uzależnione są od jednoczesnego działania dwóch lub większej liczby czynników.

Przyjmując, że ceny akcji reagują równocześnie na dwa czynniki (np. na zmiany ogólnej koniunktury rynku akcji oraz zmiany produkcji przemysłowej), to stopę zwrotu z akcji J w okresie t można zapisać według następującego wzoru:

gdzie:

- rynkowa beta akcji J (siła reakcji stopy zwrotu akcji J na zmiany rynku),

- stopa nieoczekiwanego wzrostu produkcji przemysłowej w okresie t,

- siła reakcji stopy zwrotu z akcji J na nieoczekiwane zmiany produkcji przemysłowej.

Jeżeli założymy, że stopa zwrotu z rynku nie jest skorelowana ze stopą nieoczekiwanego wzrostu produkcji przemysłowej, to wariancję portfela będziemy mogli zapisać za pomocą następującego wzoru:

=
+
+

Jeżeli dalej założymy, że składniki resztowe akcji wchodzących w skład portfela nie są ze sobą skorelowane, to wariancję resztową portfela można obliczyć według następującego wzoru:

Wzór ten opiera się na założeniu, że model wielowskaźnikowy uwzględnia wszystkie czynniki wywołujące korelację stóp zwrotu z poszczególnych akcji.

Identyfikacja tych czynników, które mogą powodować zmiany rynkowych cen akcji jest zadaniem stosunkowo trudnym.

W formie hipotezy można przyjąć, że wskaźnikami makroekonomicznymi, które mogą wpływać na ceny wszystkich akcji są:

1. stopa inflacji,

2. stopa wzrostu produkcji przemysłowej,

3. stopa bezrobocia,

4. deficyt bilansu handlowego,

5. kurs walutowy,

6. stopa procentowa.

Jeżeli zidentyfikujemy czynniki, które wpływają na stopy zwrotu z poszczególnych akcji, to włączając te czynniki do modelu możemy sformułować wzór na oczekiwaną stopę zwrotu z portfela w modelu wielowskaźnikowym, który ma następującą postać:

gdzie:

- współczynnik beta portfela wyznaczony względem pierwszego wskaźnika,

- oczekiwana zmiana pierwszego wskaźnika w ciągu następnego okresu.

Z kolei wariancję stopy zwrotu z portfela w modelu wielowskaźnikowym można zapisać za pomocą następującego wzoru:

=
+
+ ...+
+

Wzór ten zawiera N składników reprezentujących ryzyko systematyczne związane z poszczególnymi czynnikami uwzględnionymi w modelu oraz wariancję resztową.

Porównanie modelu Markowitza i modeli wskaźnikowych

1. Zarówno model Markowitza jak i modele wskaźnikowe służą wyznaczaniu zbioru minimalnego ryzyka. Modele te posługują się jednak odmiennymi formułami wyznaczania wariancji portfela.

Formuła Markowitza jest absolutnie dokładna; modele wskaźnikowe dają jedynie przybliżone wyniki.

2. Model Markowitza nie czyni żadnych założeń co do źródeł korelacji pomiędzy poszczególnymi akcjami - mogą się one kształtować pod wpływem dowolnej liczby dowolnych czynników.

Natomiast u podstaw modeli wskaźnikowych leży założenie, że poszczególne elementy macierzy kowariancji są całkowicie zdeterminowane tym, że ceny wszystkich akcji reagują podobnie na działanie pewnej liczby czynników. To z kolei prowadzi do wniosku, że składniki resztowe poszczególnych akcji nie są ze sobą skorelowane.

3. Obliczenie wariancji portfela w oparciu o procedurę zaproponowaną przez Markowitza jest co prawda dokładne, ale czasochłonne.

Modele wskaźnikowe upraszczają istotnie procedurę obliczeń, ale nie dają gwarancji, że zestawione za ich pomocą portfele będą rzeczywiście portfelami minimalnego ryzyka.

4. Wyniki badań empirycznych dowodzą, że korelacje pomiędzy składnikami resztowymi poszczególnych akcji wyrażają się liczbami dodatnimi. W konsekwencji wariancja portfela obliczona za pomocą modelu jednowskaźnikowego będzie zaniżona w stosunku do wariancji rzeczywistej.

5. Problem korelacji składników resztowych można ograniczyć budując modele wielowskaźnikowe. Wprowadzając nowe zmienne niezależne do modelu zwiększamy tym samym jego moc objaśniającą.

6. W praktyce zarządzania portfelem inwestycyjnym bardziej rozbudowany i ogólniejszy model Markowitza służy jako narzędzie alokacji posiadanych funduszy pomiędzy szerokie klasy aktywów kapitałowych, takie jak akcje (ogół akcji), obligacje, nieruchomości itp.

Po określeniu, na podstawie modelu Markowitza, jaką część kapitału należy przeznaczyć na przykład na inwestycje w akcje, zarządzający portfelem wykorzystują modele wskaźnikowe w celu dokonania wyboru akcji konkretnych spółek i określenia jaką część kapitału zainwestować w akcje każdej wybranej spółki.

Ogólnie biorąc, modele wskaźnikowe służą optymalizacji portfela w ramach każdej z szerokich klas aktywów, przy czym najczęściej wykorzystywane są w odniesieniu do akcji.

---