III. Ograniczanie ryzyka - teoria portfela Markowitza

Portfel inwestycyjny jest kombinacją różnych rodzajów papierów wartościowych (ewentualnie również aktywów rzeczowych) posiadanych przez inwestora.

Celem analizy portfelowej jest taki dobór papierów wartościowych do portfela, aby spełnione były jednocześnie kryteria najwyższej możliwej stopy zwrotu i najniższego możliwego ryzyka.

Podstawy teorii portfela (teorii portfelowej) stworzył amerykański ekonomista Harry Markowitz (nagroda Nobla w 1990 r.).

Markowitz opracował sposób ilościowej analizy zależności między stopą zwrotu i ryzykiem portfela (artykuł „Portfolio Selection” opublikowany w 1952 r.).

Teoria portfelowa Markowitza została zbudowana na połączeniu stopy zwrotu z wariancją.

Inwestorzy, dokonując racjonalnych wyborów, postrzegają oczekiwaną stopę zwrotu portfela jako rzecz pożądaną oraz wariancję stopy zwrotu jako efekt niepożądany.

W swojej teorii Markowitz:

1. przeszedł od analizy pojedynczych papierów do analizy ich zestawu, czyli portfela,

2. wskazał na kluczową rolę ryzyka w procesie inwestycyjnym,

3. ujął dochód i ryzyko portfela w formuły matematyczne.

Pytanie - jak zachowują się oczekiwane stopy zwrotu oraz ryzyko portfela składającego się z wielu papierów wartościowych?

W praktyce najczęściej mamy do czynienia z portfelami wieloskładnikowymi - portfel posiada tyle składników, ile rodzajów papierów w nim występuje.

Kowariancja jest miarą statystyczną, która pozwala określić w jaki sposób stopy zwrotu z dwóch walorów są powiązane między sobą (współzależne).

Kowariancję można wyliczyć za pomocą następujących wzorów:

1. kowariancja w populacji generalnej

2. kowariancja z próbki

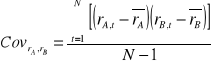
Kowariancja jest wielkością nieograniczoną; może przyjmować wartości z przedziału od minus do plus nieskończoności.

Istnieje jednak możliwość standaryzacji kowariancji poprzez jej podzielenie przez iloczyn odchyleń standardowych stóp zwrotu z obu inwestycji. Otrzymujemy w ten sposób współczynnik korelacji:

Współczynnik korelacji stóp zwrotu akcji określa siłę i kierunek powiązania stóp zwrotu tych akcji. Współczynnik ten przyjmuje wartości z przedziału od -1 do +1.

Oczekiwaną stopę zwrotu portfela składającego się z wielu aktywów można obliczyć według następującego wzoru:

gdzie:

- oczekiwana stopa zwrotu portfela,

- udział j-tej akcji w portfelu,

M - liczba składników portfela.

Bardzo ważną charakterystyką portfela są udziały (wagi) poszczególnych składników w portfelu.

Udziały oblicza się jako stosunek wartości poszczególnych akcji będących składnikami portfela do wartości całego portfela (a nie ich ilości).

Przykład

1) Inwestor posiada 100 akcji firmy A i 100 akcji firmy B. Aktualna cena akcji A wynosi 5 zł, natomiast akcji B 10 zł.

Wartość portfela:

akcje A: 100 × 5 zł = 500 zł

akcje B: 100 × 10 zł = 1000 zł

portfel 1500 zł

Udziały poszczególnych akcji w portfelu wynoszą odpowiednio: x_A=0,3333 oraz x_B=0,6667.

Udziały składników w portfelu mogą zmieniać się w sytuacji, gdy inwestor nie dokonuje żadnych transakcji - tylko na skutek zmiany cen walorów.

2) Załóżmy, że w przedstawionym przykładzie cena akcji A wzrosła do 6 zł a cena akcji B spadła do 9 zł.

Wartość portfela:

akcje A: 100 × 6 zł = 600 zł

akcje B: 100 × 9 zł = 900 zł

portfel 1500 zł

Udziały poszczególnych akcji w portfelu wynoszą odpowiednio: x_A=0,4 oraz x_B=0,6.

Zmiany cen papierów wartościowych będących składnikami portfela mogą powodować także wzrost lub spadek wartości portfela.

3) Załóżmy, że cena akcji A spadła do 4 zł a cena akcji B wzrosła do 12 zł.

Wartość portfela:

akcje A: 100 × 4 zł = 400 zł

akcje B: 100 × 12 zł = 1200 zł

portfel 1600 zł

Wartość portfela zwiększyła się do 1600 zł (wzrost o 6,67%), udział akcji A w portfelu spadł (x_A=0,25), natomiast udział akcji B wzrósł (x_B=0,75).

4) Załóżmy, że cena akcji A wzrosła do 6 zł a cena akcji B spadła do 8 zł.

Wartość portfela:

akcje A: 100 × 6 zł = 600 zł

akcje B: 100 × 8 zł = 800 zł

portfel 1400 zł

Wartość portfela zmniejszyła się do 1400 zł (spadek o 6,67%), udział akcji A w portfelu wzrósł (x_A=0,4286), natomiast udział akcji B spadł (x_B=0,5714).

Suma wag (udziałów) wszystkich walorów wchodzących w skład portfela zawsze równa jest 1 (lub 100%).

Z kolei wagi poszczególnych walorów w portfelu mogą być dodatnie lub ujemne. Ujemna waga pojawia się w przypadku krótkiej sprzedaży.

Krótka sprzedaż jest to sprzedaż akcji pożyczonych od osoby trzeciej - najczęściej od biura maklerskiego.

Krótkiej sprzedaży inwestor dokonuje w sytuacji, gdy przewiduje spadek cen walorów i tym samym możliwość ich odkupienia w przyszłości po niższej cenie.

Po upływie ustalonego okresu czasu kupuje pożyczoną ilość akcji i oddaje je właścicielowi.

Przykład

Inwestor posiada własne 1000 zł i dodatkowo dokonuje krótkiej sprzedaży akcji firmy B za 500 zł. Uzyskane pieniądze wraz z własnymi (łącznie 1500 zł) przeznacza na zakup akcji firmy A.

Wagi (udziały) poszczególnych akcji w portfelu wynoszą: x_A= 1,5 oraz x_B= -0,5.

Obliczenie ryzyka portfela jest trudniejsze niż oczekiwanej stopy zwrotu.

Do obliczenia ryzyka portfela konieczna jest znajomość macierzy kowariancji, nazywanej także macierzą wariancji-kowariancji.

Akcja	A	B
A B	Cov(rA,rA) Cov(rA,rB)	Cov(rB,rA) Cov(rB,rB)

Kowariancja stopy zwrotu akcji z nią samą równa jest wariancji stopy zwrotu tej akcji:

Do obliczenia wariancji z portfela niezbędna jest także znajomość udziałów poszczególnych akcji w portfelu.

Akcja		xA A	xB B
xA xB	A B	Cov(rA,rB)	Cov(rB,rA)

W przypadku portfela dwuskładnikowego jeżeli udział akcji A w portfelu wynosi x_A, to udział akcji B równy jest x_B=1 - x_A.

Mnożąc każdy z elementów macierzy przez iloczyn udziałów akcji, dla których dana kowariancja jest obliczana oraz dodając do siebie uzyskane rezultaty otrzymujemy wzór na wariancję portfela składającego się z akcji dwóch spółek:

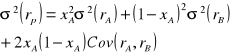
Kowariancję między dwiema zmiennymi możemy zapisać według następującego wzoru:

a zatem:

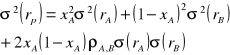
Wzór na wariancję portfela możemy uogólnić dla więcej niż dwóch walorów.

W przypadku portfela trzyskładnikowego, składającego się z akcji firm A, B i C, wzór wygląda następująco:

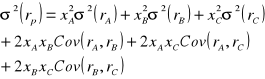
Wzór ten możemy uogólnić na dowolną liczbę akcji:

J
I

Ze względów praktycznych często wygodniej jest posługiwać się odchyleniem standardowym, które jest pierwiastkiem kwadratowym z wariancji:

Współczynnik korelacji może przyjmować wartości z przedziału -1,+1, dlatego rozważymy trzy hipotetyczne sytuacje, gdy współczynnik ten kształtuje się odpowiednio na poziomie +1, 0 i -1.

1) Dla współczynnika korelacji równego 1, wyrażenie na odchylenie standardowe portfela składającego się z dwóch akcji uprości się do następującej postaci:

2) Gdy współczynnik korelacji wynosi zero, to wyrażenie na odchylenie standardowe portfela składającego się z dwóch akcji ma postać:

3) Gdy współczynnik korelacji równy jest -1, to wyrażenie na odchylenie standardowe portfela składającego się z dwóch akcji uprości się do następującej postaci:

Charakterystyki portfela (czyli stopa zwrotu i ryzyko) wynikają z parametrów poszczególnych papierów wartościowych wchodzących w jego skład oraz ich udziałów (wag) w portfelu.

Inwestorzy nie mają możliwości zmiany oczekiwanych stóp zwrotu ani odchylenia standardowego walorów wchodzących w skład portfeli, ale mogą zmieniać udziały poszczególnych składników w swoich portfelach.

Powstaje w związku z tym pytanie, co takie zmiany powodują?

Przykład

Akcje dwóch firm A i B charakteryzują się następującymi oczekiwanymi stopami zwrotu i odchyleniem standardowym:

=0,15;
=0,075;
=0,25;
=0,125

1) doskonała korelacja dodatnia: ρ=1

=

+

=

2	0,225	0,375
1	0,15	0,25
0,75	0,131	0,218
0,5	0,112	0,187
0,333	0,099	0,166
0,25	0,093	0,156
0	0,075	0,125

2) brak korelacji: ρ=0:

=

+

=

2	0,225	0,515
1	0,15	0,25
0,75	0,131	0,190
0,5	0,112	0,139
0,333	0,099	0,117
0,25	0,093	0,112
0	0,075	0,125

3) doskonała korelacja ujemna: ρ= -1

=

+

=

2	0,225	0,625
1	0,15	0,25
0,75	0,131	0,156
0,5	0,112	0,062
0,333	0,099	0
0,25	0,093	0,031
0	0,075	0,125

Można obliczyć udziały poszczególnych akcji, dla których odchylenie standardowe portfela wynosi zero.

W przypadku portfela dwuskładnikowego wzory są następujące:

σ_B σ_A

X_A = ---------- oraz X_B = 1 - X_A = ---------

σ_A + σ_B σ_A + σ_B

W naszym przykładzie udziały akcji A i B wynoszą:

x_A = 0,333 (=0,125/0,375) oraz x_B = 0,667 (=0,25/0,375).

W celu ograniczenia ryzyka inwestor powinien wybierać do portfela papiery wartościowe o niskich dodatnich, zerowych lub (najlepiej) ujemnych współczynnikach korelacji pomiędzy stopami zwrotu.

Im mniejsza korelacja pomiędzy składnikami portfela, tym większy jest stopień zredukowania jego ryzyka, czyli tym większe potencjalne korzyści z jego dywersyfikacji.

Wnioski:

1) Stopa zwrotu portfela, niezależnie od udziałów poszczególnych akcji, zawsze jest nie mniejsza niż najniższa stopa zwrotu i nie większa niż najwyższa stopa zwrotu akcji będących składnikami portfela.

2) Podstawowe znaczenie dla poziomu ryzyka portfela (mierzonego odchyleniem standardowym oczekiwanej stopy zwrotu) ma wartość współczynnika korelacji pomiędzy zmianami oczekiwanych stóp zwrotu akcji wchodzących w skład tego portfela.

3) Pomijając możliwość krótkiej sprzedaży, należy stwierdzić że:

• w przypadku doskonałej korelacji dodatniej (ρ=1) żadna kombinacja udziałów akcji A i B nie przyczynia się do ograniczenia poziomu ryzyka portfela (poniżej ryzyka wchodzących w jego skład akcji);

• jeżeli akcje A i B nie są ze sobą skorelowane (ρ=0) to można skonstruować portfel, którego ryzyko jest mniejsze od ryzyka wchodzących w jego skład akcji;

• w przypadku doskonałej korelacji ujemnej (ρ=-1) istnieje możliwość skonstruowania z akcji A i B (czyli papierów wartościowych obciążonych ryzykiem) takiego portfela, dla którego odchylenie standardowe równe jest zero; tzn. za pomocą dywersyfikacji można całkowicie wyeliminować ryzyko portfela.

---