|
Temat ćwiczenia: Układy logiczne kombinacyjne. |
1. Wprowadzenie.
Układami logicznymi - funktorami lub bramkami - nazywa się układy realizujące funkcje oparte na algebrze Boola. W układach logicznych wartości występujących sygnałów przyjmują pewne dozwolone poziomy dyskretne, co stanowi jedną z najbardziej charakterystycznych ich cech.
Niemal wyłącznie są stosowane układy logiczne binarne (dwójkowe, zero-jedynkowe), w których sygnały mogą przyjmować tylko dwie wzajemne wykluczające się wartości logiczne: wartość „zero” (0) i wartość „jeden” (1).
Logika binarna w naturalny sposób opisuje działanie wielu urządzeń technicznych, np. stary „0” i „1” mogą być odpowiednikami stanu „wyłączenia” i „włączenia” elementarnego przełącznika elektrycznego. Przez swoje liczne analogie i zastosowania w odniesieniu do urządzeń zawierających przełączniki, teoria układów logicznych bywa nazywana teorią układów przełączających. Odpowiednio, funkcje logiczne są nazywane funkcjami przełączającymi.
Wszystkie funkcje logiczne daje się realizować przy pomocy tylko trzech funkcji podstawowych: negacji, sumy i iloczynu. Stosując prawo de Morgana oraz prawo podwójnej negacji można zrealizować dowolny układ logiczny jedynie z funkcji iloczynu i negacji lub sumy i negacji. Taki zestaw funkcji, za pomocą którego można zrealizować wszystkie inne funkcje, nazywa się zestawem funkcjonalnie pełnym. Jednak realizacja wszystkich funkcji logicznych przy użyciu dwu lub trzech funkcji podstawowych, choć możliwa, nie jest jednak optymalna. Dlatego w praktyce, w celu minimalizacji liczby elementów logicznych, wykorzystuje się wiele gotowych układów realizujących często bardzo skomplikowane funkcje.
2. Cel ćwiczenia.
Celem ćwiczenia było poznanie właściwości układów kombinacyjnych na podstawie dwóch zaprojektowanych przez nas układów:
Translator kodu „1 z 8” na kod binarny
Sumator
3. Projekt translatora kodu „1 z 8” na kod binarny
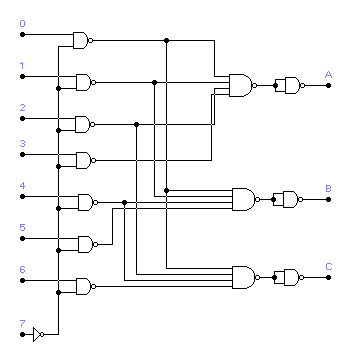
3.1. Schemat translatora kodu „1 z 8” na kod binarny
4. Projekt sumatora.
A |
B |
C |
|
X |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
Schemat sumatora.
Wyniki otrzymane w czasie badania układów.
5.1. Translator kodu „1 z 8” na kod binarny.
Sumator.
A |
B |
C |
|
X |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
Wnioski.
Bramka logiczna jest najprostszym układem kombinacyjnym. Układy kombinacyjne realizują funkcje logiczne; wartość zmiennej wyjściowej zależy w nich wyłącznie od aktualnej kombinacji zmiennych wejściowych.
Ćwiczenie to, pozwoliło nam poznać idee elementów logicznych, a także realizowanie działań arytmetycznych takich jak: dodawanie, odejmowanie, mnożenie, dzielenie.
Celem zajęć laboratoryjnych było przeprowadzenie ćwiczeń na układach logicznych kombinacyjnych. Zaprojektowanymi i wykonanymi układami były: sumator i translator kodu „1 z 8” na kod binarny. Obydwa układy działały bez zarzutu. Wyniki przez nas otrzymane jak i wcześniej obliczone w zupełności się zgadzają co świadczy o poprawności obliczeń jak i poprawności zmontowanego układu w czasie ćwiczeń. Staraliśmy się by wykonane przez nas projekty składały się z jak najmniejszej ilości użytych bramek i dzięki temu zyskać przejrzystość projektu. Pomimo tego zbudowane dekodery były i tak dosyć „obszernymi” układami. Obecnie nie projektuje się już takich rzeczy, tylko kupuje się już gotowe układy scalone. Dobrym też rozwiązaniem, jeśli na rynku nie ma interesującego nas układu, jest użycie programowalnego układu GAL. Umożliwia on jeszcze większe zminimalizowanie ilości użytych elementów w budowanym urządzeniu. Ilość kombinacji przy projektowaniu urządzeń jest praktycznie nieograniczona. Możliwość łączenia elementów kaskadowo, np. sumatorów logicznych zwiększa ilość bitów porównywanych do interesującej nas liczby, ale za to czas odpowiedzi sygnału na wyjściu przedłuża się wraz z ilością użytych szeregowo elementów. Każdy więc projektując jakiekolwiek urządzenie cyfrowe może go zbudować bez większych problemów.
Układy kombinacyjne ze względu na swoje możliwości szerokie zastosowanie znalazły w układach sekwencyjnych i są produkowane w zwartych blokach zwanych mikroprocesorem.
WYKAZ LITERATURY
[1] Horowitz P.; Hill W.: Sztuka elektroniki. Warszawa, 1999.
[2] Turczyński J.; Piekoń J.: Układy scalone TTL w systemach cyfrowych.
[3] Chwaleba A.; Moeschke B.; Płoszajski G.: Elektronika. WSP. Warszawa, 1998.
4
8 |
|
3 |
|||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
A |
B |
C |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
8 |
|
3 |
|||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
A |
B |
C |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
Wyszukiwarka
Podobne podstrony:
Kombinacyjne uklady logiczne
Układy logiczne, Logiczny układ kombinacyjny
Kombinacyjne uklady logiczne
sprawozdanie układy logiczne ćw 4
SYNTEZEAUTOMATU, ☆☆♠ Nauka dla Wszystkich Prawdziwych ∑ ξ ζ ω ∏ √¼½¾haslo nauka, Logika, układy LOGI
układy logiczne, ptul2, Tablice Karnaugha
Układy logiczne
Elementarne uklady logiczne
Układy logiczne cz.2, Laboratorium układów elektronicznych
Elektronika- Układy logiczne cz.1- dekodery, trans-latory.DOC, Wydz. E i A Grupa
Elektronika- Układy logiczne cz.1- dekodery, trans-latory.DOC, Wydz. E i A Grupa
Programowalne uklady logiczne
UKŁADY LOGICZNE
11 PEiM Układy logiczne doc (2)
07 Podstawowe uklady logiczne (2)
więcej podobnych podstron