60490

Kartografia matematyczna. Odwzorowanie Gaussa Krugera

Wzory odwzorowania Gaussa-Krugera (B,I. —> X,Y)

Element luku: ds² =(MdB)² +(NcosBdL)²- na elipsoidzie,

dS² =dx² +dy²    - na płaszczyźnie

Uwaga: Inki odpowiadające równym przyrostom argumentów 8 i L nie są sobie równe. Wprowadzimy szerokość izometryczną q:

dq =

MdB

Ncos B ażeby: ds =N cos B-Jdq^: -t-dL^:

Szerokość izometryczną sprawia, że otrzymujemy równe wartości łuków południka i równoleżnika dla równych przyrostów dq i dL.

,    .    dS

ds

Wykorzystując fakt, że dq i dL są różniczkami niezależnych zmiennych 8 i L można zapisać skalę jako funkcję zmiennych zespolonych:

2 _    1    (dx + idy)(dx - idy)

N² cos² 8 (dq + idL)(dq - idL)

Warunek równokątności odwzorowania oznacza, że skale są niezależna od azymutu elementów liniowych dS i ds (równe w każdym punkcie)

Wyrażenie opisujące skalę można zapisać:

* +    + i 0    oraz x-iy=f(q-il)

gdzie f- funkcja analityczna

Zakładając, że

y- 0 dla 1=0 x=f(q) dla y=0

warunkiem odwzorowania jest x = S - długość łuku południka osiowego tzn. odcięte muszą być równe długości łuku południka.

Po rozwinięciu w szereg Taylora funkcji f(q⁺ il) względem U otrzymamy:

x + iy = S + i/^^S + ⁴    +...gdzie S = x_lm0 - długość łuku połud. osiowego do szerokości B.

dq 2 dq

Po oddzieleniu części rzeczywistej od urojonej i wprowadzeniu:

— =N cos B    d*s _ d ( ds

dq    ’    dq dB dq    dq² dB \ dq

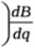
otrzymamy:

x = S+—NsinBcosB + — NsinBcos*B(5-t² +9^² +4^²)-t*.

2