60747

1.Przykładowe zagadnienia i wykładu.

1.    Zapisać definicję białego szumu w ścisłym sensie.

2.    Podać definicję procesu liniowego. Kiedy proces liniowy jest kowariancyjnie stacjonarny ?

3.    Podać definicję procesu liniowego ze średnią p

4.    Podać definicję procesu średniej ruchomej MA(q)

5.    Podać definicję procesu ARMA(p,q)

6.    Zdefiniować wielomian opóźnień L (lag operator), a następnie zapisać przy jego pomocy proces ARMA(p,q)

7.    Podać przykład procesu, któiy jest ściśle stacjonarny a nie jest kowariancyjnie stacjonarny

8.    Podać przykład procesu, który jest kowariancyjnie stacjonarny, a nie jest ściśle stacjonarny

9.    Podać przykład procesu, który jest kowariancyjnie i ściśle stacjonarny.

10.    Wyprowadzić warunki stacjonarności procesu AR(1)

11.    Wyprowadzić warunki stacjonarności procesu AR(2)

12.    Wyprowadzić warunki stacjonarności procesu MA(1)

13.    Wyprowadzić warunki stacjonarności procesu ARMA(1,1)

14.    Podać przykład procesu, który jest 1(3)

15.    Podać przykład procesu, który jest 1(2)

16.    Niech {z,, t e Z) będzie procesem AR(1), tj. z, =</>z,__l +£,, {£•, }~WN(0, <r).

Wiedząc, że Cov(z,, z,^) = 0*'

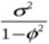
dla |0 < 1, Jc€ Z\{0}, obliczyć Cov(z_f,z_f_*)

dla |0|>1.

17.    Niech {zt, t e Z) będzie procesem AR(1), tj. z, =<pz_l__l +£,, {£, }~WN(0, a²). Wiedząc, że Cor^z^z,^) dla |0| < 1, ke Z\{0), obliczyć

p(/i)=Corr(z_lfz,^) dla |<j>| > 1.

18.    Dla procesu AR(1) z warunkiem początkowym omówić wpływ warunku początkowego na wartość procesu w chwili t

19.    Niech V t e N z, =(/>z,__l +£*,, {$ }~WN(0, o²), |<j>| > 1. Obliczyć : E(z, \ zo) oraz Var(z, | Zo)

20.    Niech Vfe N z, =<f>z_t__x +e,, {£•, }~WN(0, a²), |0| > 1. Czy istnieje (i jest skończona) wariancja bezwarunkowa procesu {z,} ?

a) Jeśli TAK, to czy następujące rozumowanie jest poprawne:

Var(z_f) = Var(<fe,_, +£•,)=* Var(z_t) = <pi¹Var(z,__l) + Var(£,) <=> m₂ =(f>²m₂ +<T² stąd

Var(z,) = m₂ =—j 1-0

•    Jeżeli TAK, to odpowiedź bardzo krótko uzasadnić

•    Jeśli NIE, to wskazać miejsce, w którym popełniono błąd oraz podać poprawne rozumowanie

b) Jeśli wariancja bezwarunkowa NIE istnieje, to bardzo krótko uzasadnić dlaczego.

21. Przyjmując, że z, =0.5 z,_, +£, dla t e N, obliczyć (jeśli istnieją) E(z, | z₀) oraz Var(z, | Zo)