63121

SPRAWOZDANIE

Wyznaczanie rozkładów prędkości i współczynników de Saint Yenanta w kanale otwartym (a)

1 Cel ćwiczenia

Celem ćwiczenia jest określenie profili prędkości przy przepływie w kanale otwartym dla wybranych pionów i poziomów analizowanego przekroju pomiarowego oraz wykreślenie izotach dla tego przekroju.

2. Krótkie wprowadzenie teoretyczne na temat przyczyn określania współczynników a i p, metod wyznaczania oraz zasada działania rurki Prandla

W obliczeniach projektowych kanałów otwartych często rozważany jest przypadek jednowymiarowego przepływu ustalonego. Do odwzorowania takiego przepływu najczęściej stosowany jest jednowymiarowy model przepływu cieczy lepkiej. Jego podstawę stanowią równanie ciągłości przepływu:

Q= J vdF=v_irF — cofist

A

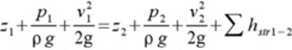
(gdzie A jest polem przekroju poprzecznego strumienia, v-prędkością, natomiast V* - średnią prędkością przepływu w kanale), oraz równanie Bemoulliego dla cieczy lepkiej, które można zapisać w postaci:

(gdzie z określa wzniesienie punktu nad przyjętym poziomem porównawczym, p jest ciśnieniem, p gęstością cieczy, v prędkością, Ilw; określa wysokość strat energii mechanicznej na odcinku między punktami 1 i 2). Analizowanie poszczególnych linii prądu jest niewygodne, a często wręcz niemożliwe. Najczęściej stosuje się równanie Bemoulliego dla całego strumienia cieczy. W przypadku strumienia wielkości charakteryzujące przepływ mogą przyjmować zróżnicowane w^rartości w obrębie jednego przekroju poprzecznego. W związku z nierównomiernym rozkładem prędkości w przekroju poprzecznym, przy zastosowaniu równania Bemoulliego dla całego strunrienia pojawia się problem, w jaki sposób uwzględrrić nierówmonriemy rozkład prędkości i jednocześnie wyznaczyć reprezentujące cały przekrój prędkości występujące w członach związanych z energią kinetyczną. Ta sama kwestia dotyczy sposobu określenia reprezentatywnych dla całego przekroju wartości ciśnienia oraz wielkości z występujących w równaniu Bemoulliego. Jeśli za reprezentatywne uznamy w^fartoścr członów trójmianu Bemoulliego uśrednione względem stnunienia masy, wówczas każda wielkość w trójmianie Bemoulliego mirsi zostać uśredniona zgodnie z formulą:

w =---—— I p \vvdF

Pir^ifP A

gdzie w jest średnią w stnunienia masy wartością wielkości w, p