65571

A. Zaborski. Belki ukośne

cos a 2

Q(x) = V. cos a + H _Asin a —cos ar cos ar

= -r. sin ar-// ,cosar + —■-—sinar cos a

dMls)

-=--=cosar-

ds dx di    dx

Zadanie, po odpowiednim przeliczeniu intcasywności obciążenia ciągłego (z warunku równości wypadkowych), można obliczać jak w przykładzie I.

Obliczenia w układzie współrzędnych związanym z osią belki są mniej wygodne:

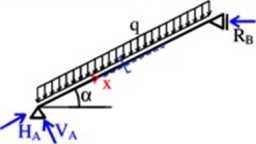
M(x) = V_Ax-qx-

Q(x) = V_A-qxcosa N(x) = -H _A + ąxsina „    _ ql(lcosa)

nu "    ₀

4. Obciążenie prostopadle do osi belki, intensywność obciążenia podana na metr bieżący belki

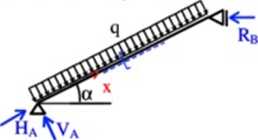
Mi _X)-V_AX-2y

Q(x) *V_A-qx N(x) = -H _A

Mn

.ąf

W „normalnym" układzie współrzędnych, niezwiązanym z osią belki:

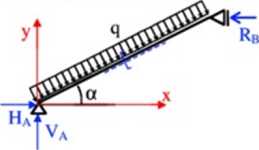
moment zginający zapisze się:

\Hx)=V_Ax-H_Ay-q *    *    = V_Ax-H    .

cos a 2 cos a    z^cosary

Zadanie powyższe można zastąpić równoważnym: