68235

Przykład 12.8

Akrohau wykonujący skok z poczwórnym saltem, musi zostać pochwycony przez partnera po czasie / — 137 s od oderwania się od trapezu. Załóżmy, że pierwsze i ostatnie ćwierć obrotu wykonuje on w pozycji wyprostowanej (patrz rysunek 12.20). gdy jego moment bezwładności względem środka masy (oznaczonego kropką) jest równy Ą = 19.9 kg • m², a pozostałą część Inni odbywa w pozycji skurczonej, gdy ma moment bezwładności /j = 3.93 kg • m³. Ile musi wynosić jego prędkość kątowa a* wokół środka masy. podczas lotu w pozycji skurczonej'*

ROZWIĄZANIE:

Oczywiście akrobata musi obracać się tak szybko, aby w wymaganym czasie 1.87 s wykonać C2tery pełne obroty ciała. W tym celu zwiększa on swoją prędkość kątową do wartości tuj. przyjmując pozycję skurczoną. Aby znaleźć związek cuj z jego początkową prędkością kątową <ui. zastosujemy następujące spostrzeżenie:

O1. W czasie całego lotu moment pędu akrobaty względem jego środka masy jest zachowany, ponieważ nie działa na niego żaden wypadkowy zewnętrzny moment siły względem jego środka masy. Korzystając z równania (12.34). zasadę zachowania momentu pędu (Li = Lj) możemy zapisać w postaci:

!\(0\ = /»«»>2.

czyli

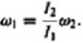
(12.36)

O-t 2. Prędkość kątową możemy wyrazić przez kąt obrotu i czas potrzebny na jego pokonanie Na początku i na końcu skoku akro-