68937

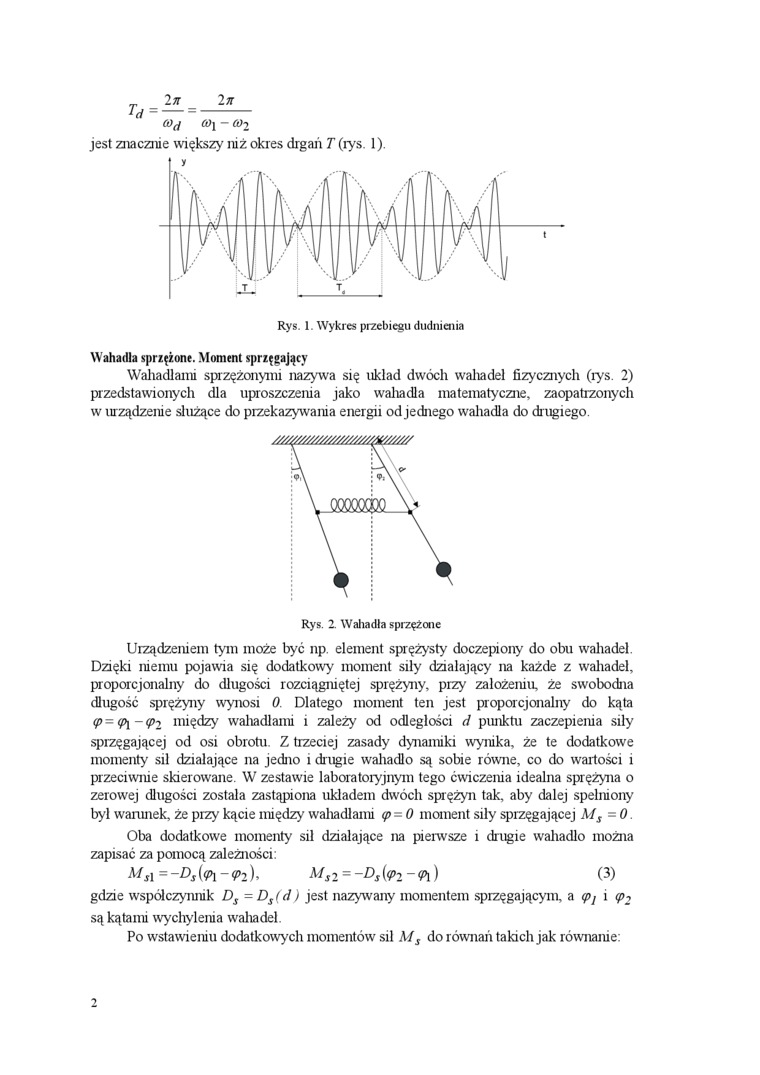
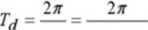
(Od (0\ - (Ol

jest znacznie większy niż okres drgań T (rys. 1).

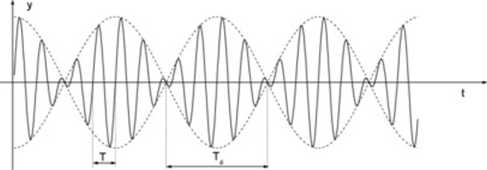
Rys. 1. Wykres przebiegu dudnienia Wahadła sprzężone. Moment sprzęgający

Wahadłami sprzężonymi nazywa się układ dwóch wahadeł fizycznych (rys. 2) przedstawionych dla uproszczenia jako wahadła matematyczne, zaopatrzonych w urządzenie służące do przekazywania energii od jednego wahadła do drugiego.

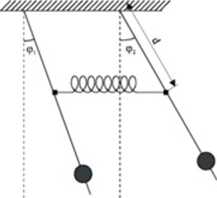
Rys. 1 Wahadła sprzężone

Urządzeniem tym może być np. element sprężysty doczepiony do obu wahadeł. Dzięki niemu pojawia się dodatkowy moment siły działający na każde z wahadeł, proporcjonalny do długości rozciągniętej sprężyny, przy założeniu, że swobodna długość sprężyny wynosi 0. Dlatego moment ten jest proporcjonalny do kąta (p=(p\-(pi między wahadłami i zależy od odległości d punktu zaczepienia siły sprzęgającej od osi obrotu. Z trzeciej zasady dynamiki wynika, że te dodatkowe momenty sil działające na jedno i drugie wahadło są sobie równe, co do wartości i przeciwnie skierowane. W zestawie laboratoryjnym tego ćwiczeiua idealna sprężyna o zerowej długości została zastąpiona układem dwóch sprężyn tak, aby dalej spełniony był warunek, że przy kącie między wahadłami <p = 0 moment siły sprzęgającej M_s = 0.

Oba dodatkowe momenty sil działające na pieiwsze i drugie wahadło można zapisać za pomocą zależności:

M_s\=-^Ds(<h.-9l)> M_si = —D_s {(pi - (p\)    (3)

gdzie współczynnik D_s =D_s(d) jest nazywany momentem sprzęgającym, a q>j i q>₂ są kątami wychylenia wahadeł.

Po wstawieniu dodatkowych momentów sil M_s do równań takich jak równanie:

2