71881

Krok 2. Całkowanie metodą Simpsona

Matematyczny opis metody

Całka obliczana jest dla prostej funkcji podcałkowej /U)

b

\f(x)d.\    (!)

a

gdzie a < b (granice całkowania).

Przybliżoną wartość całki oblicza się na podstawie wzoru Simpsona.

Dany przedział («. b) dzieli się na trzy równe podprzedziały:

(<**•*,! ® U, »*il. Ui.^l. [x₂.x₃] = [x_y b].    (2)

W kolejnych podprzedzialach stosujemy wór Simpsona

= '' |/(.v,) + 4/(.t, + h) + f(x,.„) = /,.    (3)

h obliczane jest jako

(4)

(5)

h = — —',/=0,U.

2

Czynność powtarzana jest w każdym podprzcdzialc. Uzyskujemy sumę:

J/(j=

fl    <-0

Następnie każdy z przedziałów dzieli się znowu na trzy części i w podobny sposób otrzymuje się drugie przybliżenie całki. Procedura ta jest kontynuowana do chwili, gdy różnica pomiędzy dworna kolejnymi przybliżeniami obliczanej całki jest dostatecznie mała lub gdy długości podprzed/ialów są mniejsze od (b-a)l3\ gdzie n oznacza zadaną liczbę naturalną.

2x

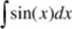
o

Przykład. Obliczyć całkę oznaczoną

» x = quad(‘sin', 0, 2*pi)

Zad 2. Obliczyć całkę oznaczoną