82373

Część 1 4. RÓWNANIE PRACY WIRTUALNEJ 7

dT(:x)

rfi

+ p(x) órU)=0

5V(.1

.x

dT{x

dT[x\

dx

+/>(*]

dx=0

(49)

J óv(x)- -~-dx + j6v{x)p(x)ck=0

o    n

W celu obliczenia całki J* 6 f'(.x)* rfx skorzystamy z twierdzenia o całkowaniu przez części.

J* tid\-=ti\'- J vfA/

M = óf(jc)    d\' =———dx

«x    rfx

'    rfx    * o    A

Równanie (4.9) uzyska więc postać:

órUir^-J*T(x)-^Ó^^X)- <k + f ó?{x)p(x)(k=0

o    <«    o

6v{l)T(l)-6v(0)T(0)-f r(.x)^£^rfx+/Sr(x)p(x)dx=0

^r.-^f-rj+j ór(x)p(x)<ń=f t(x)

d(6 f(.x)) dx

dx

(410)

Znakow^ranie: Przyjęto zasadę zgodności zwrotów sil T i Tt oraz pizemieszczeń im odpowiadającym V i Vt (rys. 4.10).

©_r

(

T

i

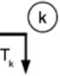
Rys. 4.10. Dodanie znroty sil poprzecznych

Znaki w wyrażeniu (4.10) wynikają z faktu, że znak dodatrn siły 7\0) jest przeciwny do założonego zwrotu siły T,, a znak dodatni siły 1\l) jest zgodny z założonym zwrotem siły 7*

«5r(.x)p(.x)rfx = j T(x

d(6V(x))

dx

dx

(4-11)

AlmaMater

Dobra D.. Jambrożek S.. Komosa M., Mikołajczak E.. Przybylska P., Sysak A.. Wdowska A.