85367

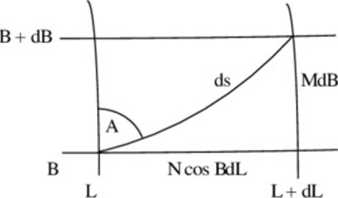
dscos A= MdB
ds sin A = N cos Bdl
dB cos A 1 ,/3 .
ds M c
dL _ sin A _ 1 ^ sin A
ds N cos B c cos B
dA dL U/ • a n
— = —sin B = -V sin AtgB
ds ds c
2V
sin Acos A
METODA ŚREDNIEJ SZEROKOŚCI GAUSSA
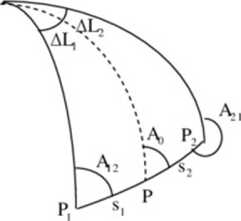
s, * s2 Al, *AL
szukane: B2. A,,
Obieramy punkt pomocniczy P . gdzie: B =
B, + B,
B, - B s2 , , ,
— = s2 cos \ - -yt(sin* Ą, + 377' cos' Ą,)-...
B. - B s.2 , , ,
——— = -s, cos Ą, —t(sin“ \ +3^'cos' \) + ..
Jeśli oba te równania raz zsumujemy, a raz odejmiemy, to: z sumy:
Wyszukiwarka
Podobne podstrony:
ł2 oznaczmy ® =—j— -L*)fvJ dsT dt V dl ds dl ds , dl czyli dv _ydv _ dl ds ds = 43 L
cyrylica pisemna da ScT B-i J i J)a ff-g Łi dCoic. 3-j, Tłu, jl/ a d/łt ^ds dl, jUj rJL. WL0„ .!«. &
Kolendowicz79 Podstawiając ds = rdm oraz ę = rsin a> otrzymujemy o (20-8) (20-9) Q = 2ngr2 sin to
fizyka006 odpowiedzi „ . m, - mAf cos« + sin«) __m 14. a=g —---^
Grupa A 1. Rozwiąż równanie 2. Rozwiąż równanie Grupa A = 7/4- X cos ■iV_ x i I i/sin x
Grupa B 1. Rozwiąż równanie Grupa B x sin " V x 2. Rozwiąż równanie + y cos x = x*yse smx. 3. R
image1488a ;c = jrcosć? - sin £ y = xsin 0 + cos#
image1670 C0S7 = M^ cd
image1670 C0S7 = M^ cd
Image1827 x = 2arctgf, dx = 2 dt 2 sin sinx =- • 2 x sin — 2 x cos — 2 cos cosx = 2 2 X cos — 2
Image241 ©/(^) = 2 A-l sin kćd + cos ki d A-l
Image241 Z Pi* = 0 ^Z P» = RD Sil1 Ó>~ RS sin a = 0 2-1 2-1Z pif =0 Z pi? = rd cos k j cose = o
więcej podobnych podstron