86762

V

COSa- —

V - V₀ cosa

Korzystamy z wzoru na prędkość w ruchu po okręgu:

V₀ - oor V « ©rcosa

Jak wynika z rysunku za r możemy podstawić A (największe wychylenie) i otrzymuje wzór na prędkość w ruchu harmonicznym.

V - AwCOSwt

Prędkość maksymalną ciała osiąga w położeniu równowagi.

Zależność prędkości od czasu w mchu harmonicznym przedstawia wykres:

Wzór na prędkość w ruchu harmonicznym można także wyprowadzić obliczając pochodną V=dx/dt.

Wykonajmy podobny rysunek i wyprowadźmy wzór na przyspieszenie w ruchu harmonicznym.

Korzystając z rysunku odczytujemy zależności:

a

sina= — a_r

Za ^ar podstawiamy wzór na przyspieszenie w mchu po okręgu:

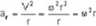
3

sra- —7-o r

a-»^Jrsinix

Otrzymujemy wzór na przyspieszenie w mchu harmonicznym:

a - -A®² sinoot a - -co²x

Znak minus oznacza, że kierunek przyspieszenia jest przeciwny względem kierunku wychylenia.

Przyspieszenie maksymalne ciało osiąga w punkcie największego wychylenia:

Zależność przyspieszenia od czasu w ruchu harmonicznym przedstawia wykres:

Wzór na przyspieszenie w ruchu harmonicznym można wyprowadzić także obliczając pochodną a=dV/dt.

Ruch drgający prosty jest ruchem niejednostajnie zmiennym.

Slla w mchu harmonicznym jest wprost proporcjonalna do wychylenia i przeciwnie

2