97192

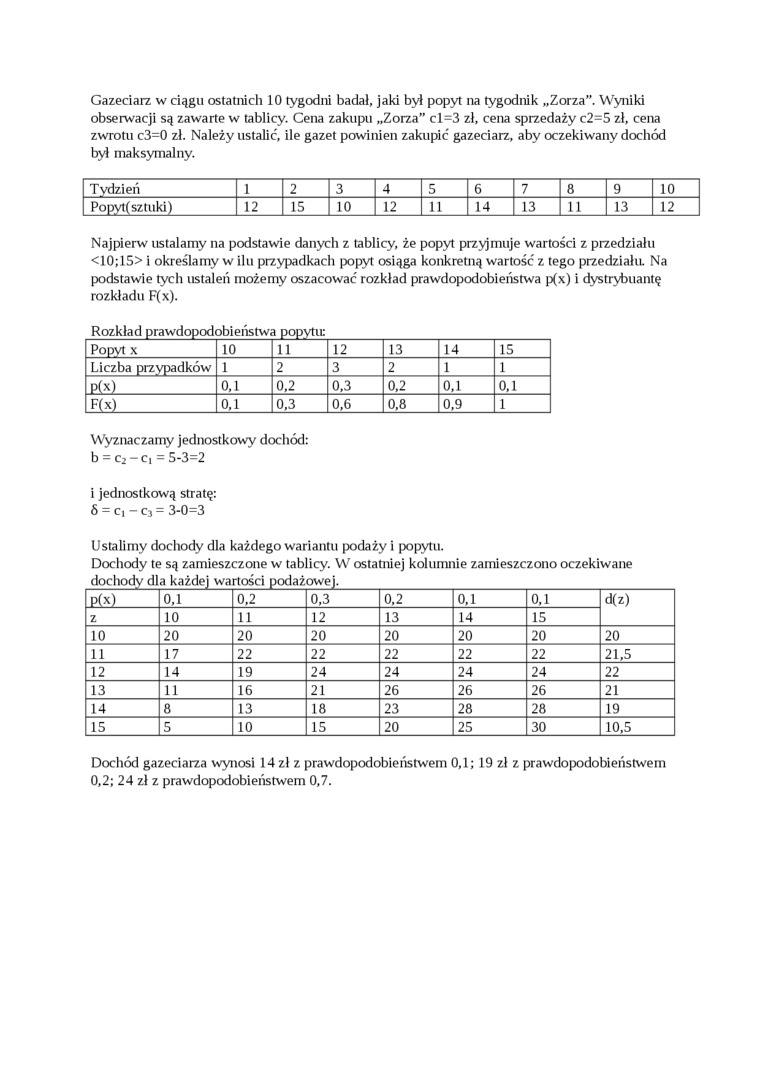
Gazeciarz w ciągu ostatnich 10 tygodni badał, jaki był popyt na tygodnik „Zorza”. Wyniki obserwacji są zawarte w tablicy. Cena zakupu „Zorza” cl=3 zł, cena sprzedaży c2=5 zł, cena zwrotu c3=0 zł. Należy ustalić, ile gazet powinien zakupić gazeciarz, aby oczekiwany dochód był maksymalny.

Tydzień	i	2	3	4	5	6	7	8	9	10
Popyt(sztuki)	12	15	10	12	11	14	13	11	13	12

Najpierw ustalamy na podstawie danych z tablicy, że popyt przyjmuje wartości z przedziału <10;15> i określamy w ilu przypadkach popyt osiąga konkretną wartość z tego przedziału. Na podstawie tych ustaleń możemy oszacować rozkład prawdopodobieństwa p(x) i dystrybuantę rozkładu F(x).

Rozkład prawdopodobieństwa popytu:

Popyt x	10	11	12	13	14	15
Liczba przypadków	1	2	3	2	1	1
p(x)	0,1	0,2	0,3	0,2	0,1	0.1
_	0,1	0,3	0,6	0,8	0,9	1

Wyznaczamy jednostkowy dochód: b = c₂ - Ci = 5-3=2

i jednostkową stratę:

6 = Cj - c₃ = 3-0=3

Ustalimy dochody dla każdego wariantu podaży i popytu.

Dochody te są zamieszczone w tablicy. W ostatniej kolumnie zamieszczono oczekiwane dochody dla każdej wartości podażowej._____>_

pM	0,1	0,2	0,3	0,2	0,1	0,1	d(z)
Z	10	11	12	13	14	15
10	20	20	20	20	20	20	20
u	17	22	22	22	22	22	21,5
12	14	19	24	24	24	24	22
13	11	16	21	26	26	26	21
14	8	13	18	23	28	28	19
15	5	10	15	20	25	30	10,5

Dochód gazeciarza wynosi 14 zł z prawdopodobieństwem 0,1; 19 zł z prawdopodobieństwem 0,2; 24 zł z prawdopodobieństwem 0,7.