3784500535

234 Jarosław Gramacki, Artur Gramacki

opisane w poprzednich rozdziałach. Następnym krokiem jest znalezienie pewnej aproksymacji tej macierzy. Uzyskujemy to poprzez zastosowanie przekształceniem SVD macierz}' TDM.

3.2.1. Przekształcenie SVD

Przekształcenie (dekompozycja) SVD jest najistotniejszym elementem analizy LSA. Polega ono na obliczeniu rozkładu macierzy A o wymiarach mxn (gdzie bez strat}' ogólności możemy założyć m >=n) w postaci iloczynu trzech macierz}^-:

^<5)

gdzie U_mxm, V_nxn są macierzami ortogonalnymi, Z_A._xA. jest macierzą diagonalną, której element}' zwane są wartościami osobliwymi (ang. singular values). Element}^- te są umieszczone na diagonalnej macierzy w kolejności malejącej. Kolumny macierzy U oraz V są zwane wektorami osobliwymi (ang. singular vectors). Kolumny macierzy U oraz V tworzą również nowe (ortogonalne) bazy dla przestrzeni kolumn / wiersz}' macierzy ,4. Interpretacja powyższego w kontekście macierzy TDM znajduje się w tabeli 7. Na rysunku 5 zilustrowano to przekształcenie w wersji pełnej (ang .fuli), cienkiej (ang. thiri) oraz przyciętej (ang. truncated) dla macierzy A o wymiarach 5x3.

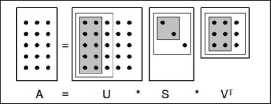
Rys. 5. Przekształcenie SVD w wersji pełnej (linia ciągła pogrubiona), cienkiej (linia ciągła cienka) oraz przyciętej do stopnia k = 2 (zaciemnienie)

Na potrzeby analiz}' LSA nie wykonuje się pokazanej powyżej pełnej wersji przekształcenia, a jedynie jego wersję przyciętą, otrzymując w ten sposób aproksymację rzędu k oryginalnej macierzy (ang. rank-k approximatioń). Zakłada się przy tym, że k < r gdzie r jest rzędem macierzy¹.

A = A_k=U_kT._kV_k^r; A_mxn, U_mxk, Z_A._xA., V^Tkxn    (6)

Matematyczne rozważania pokazują², że taka aproksymacja jest najlepsza (stąd często używana nazwa best rank-k approximation) w pewnym ścisłym matematycznym sensie i nie jest możliwe znalezienie lepszego przybliżenia macierzy A inną macierzą rzędu k. Oczywiście przycięta wersja SVD nie jest dokładną dekompozycją oryginalnej macierzy. Ale jak zostanie to pokazane, otrzymane przybliżenie jest mimo wszystko bardzo użyteczne.

Tabela 7. Interpretacja komponentów przekształcenia SVD w kontekście metody LSA

Ak	najlepsza aproksymacja rzędu k macierzy A	m	liczba termów
U	macierz wektorów termów	n	liczba dokumentów
1	macierz wartości singulamych	k	liczba czynników
V	macierz wektorów dokumentów	r	rząd macierzy A

1

   N rysunku 5 zakładamy, że macierz A jest pełnego rzędu czyli rank(A)=3.

2

   Wykazano to w 1936 roku (twierdzenie Eckarta-Younga), kiedy niewiele jeszcze myślano o prakty cznych zastosowaniach przekształcenia SVD! Patrz też opis w [Stewart93],