3826200341

str. 7

Opracowanie wyników pomiarów - oszacowanie niepewności pomiaru

E. Przykłady zastosowania reguł A,B i C

E.l Obliczenie niepewności typu A dla serii niezależnych pomiarów tej samej wielkości_|

Wielokrotnie zmierzono czas ruchu przyspieszonego ciężarków zawieszonych na nici przełożonej przez bloczek, przy tej samej przebywanej drodze s = 50 cm. Różnica mas ciężarków zawieszonych po obu stronach bloczka wynosi ok. m = 3,48 g. Pomiaru czasu dokonywano za pomocą elektronicznego stopera uruchamianego ręcznie - zarejestrowano n = 10 pomiarów czasu, po odrzuceniu wyników skrajnych, zbyt znacząco odbiegających od pozostałych i ocenionych jako pomyłkowe. Wyniki zarejestrowanych pomiarów są następujące:

i	1	2	3	4	5	6	7	8	9	10
tt [s]	4,34	4,02	4,22	4,39	4,12	4,18	4,28	4,43	4,32	4,13

Obliczone w oparciu o procedurę A.l estymaty: wartość średnia oraz odchylenia standardowe:

1 V^-"¹    Sti

t=-'2_j t( = 4,2430 s , S_ti = 0,1314s = 0,13 s , Sj = -j= = 0,04156s = 0,042 s .

Jako wynik pomiaru przyjmujemy t = t = 4,243 s oraz niepewność standardową u(t) = Sj = 0,042 s . Niepewność rozszerzoną obliczamy (zgodnie z A.4 i D.l) dla poziomu ufności p = 95% oraz liczby stopni swobody v = n — 1 = 9 otrzymując z tablic współczynnik rozszerzenia k_p = 2,32 , a zatem l/(t) = k_p • u(t) = 2,32 • 0,04156 s = 0,096 s . Wynik pomiaru czasu wraz z niepewnością rozszerzoną (dla p = 95% i k_p = 2,32): t — 4,243 s ± 0,096 s.

| E.2 Obliczanie niepewności typu A dla parametrów określających zależność liniową mierzonych wielkości

[mm]	r"i
0	0
57	20
134	40
185	60
258	80
316	100
386	120
451	140
502	160

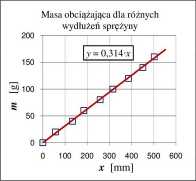
W najprostszym modelu liniowym siła obciążająca wywołuje proporcjonalne do niej wydłużenie sprężyny F₀bciaz = k ■ x, gdzie k jest współczynnikiem sprężystości sprężyny. Dla wzrastających mas zawieszanych na sprężynie otrzymujemy różne wartości siły obciążającej F₀bci_az = m ■ g i tym samym różne wydłużenia - wyniki takich pomiarów zamieszczono w tabeli obok.

Zgodnie z przyjętym modelem, zależność pomiędzy masą i wywołanym przez nią wydłużeniem jest następująca:

k    liniowa zależność

m — — ■ x -> y — a ■ x ,

9

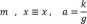
Już sama prezentacja wyników pomiaru na wykresie pokazuje, że wynikająca z modelu fizycznego zależność liniowa potwierdza się w tym doświadczeniu, przy stosowanej precyzji pomiarów. Obliczenia przeprowadzone zgodnie z A.2 (z pomocą F.l lub F.2) pozwalają określić współczynnik korelacji r = 0,99986 = 1,00, oznaczający bardzo dobrą zgodność modelu liniowego z wynikami pomiarów, a ponadto obliczyć możemy wartość współczynnika kierunkowego oraz odpowiadającą mu niepewność standardową: a = 0,314214 kg-m'¹ , u(a) = S_a = 0,0018914 kg-m'¹ przy liczbie stopni swobody v = n — 1 = 8.

Jeśli zadanie polega jedynie na wyznaczeniu współczynnika kierunkowego, to dla znanej liczby stopni swobody oraz przy poziomie ufności p = 95% wyznaczamy z tablic (D.l lub A.4) wartość współczynnika rozszerzenia, który w tym przypadku wynosi k_p = liii, a następnie obliczamy (A.2) niepewność rozszerzoną U (a) = k_p ■ u (a) otrzymując wartość U (a) = 0,004483 kgm'¹ = 0,0045 kgm'¹ , aby w rezultacie podać wynik (wg. D.3): a = (0,3142 ± 0,0045) kg-m'¹ (dla k_p = 2,37 przy p = 95%)

Jeżeli celem dodatkowym doświadczenia jest wyznaczenie współczynnika k sprężystości sprężyny, to przyjmując wartość przyspieszenia ziemskiego g = 9,811 m-s'², obliczamy zgodnie z modelem k = a ■ g oraz stosujemy regułę C.l dla złożonej niepewności standardowej u(k) = yjg² ■ u²(a) + a² • u²(g) , przyjmując niepewność standardową u(g) = (0,005 m-s'²)/V3. W rezultacie otrzymujemy: k = 3,08275 N-m'¹ , u(/c) = 0,018557 N-m'¹ oraz (przy k_p = 2,37 dla p = 95% i v = 8) obliczoną niepewność rozszerzoną U(k) = 0,04399 N-m'¹ = 0,044 N-m'¹. Ostatecznie podajemy wyznaczony współczynnik sprężystości sprężyny (zgodnie z D.3):

k = (3,083 ± 0,044) N-m'¹ (dla k_p = 2,37 przy p s= 95%)