3826200333

©msg

Opracowanie wyników pomiarów - oszacowanie niepewności pomiaru

str. 10

E.7 Przykład obliczenia złożonej niepewności standardowej dla jednokrotnych pomiarów elektrycznych

Przykład uproszczonej procedury wyznaczania wartości rezystancji poprzez pojedynczy pomiar natężenia prądu stałego oraz napięcia w takim układzie elektrycznym, kiedy mierzone napięcie jest sumą spadków napięć na mierzonym oporniku i na oporze wewnętrznym amperomierza przez który przepływa ten sam prąd, co przez badany opornik (wiemy, że wartość mierzonej rezystancji jest dużo większa od oporu wewnętrznego amperomierza R » r_A ). Wynik pomiaru oraz niepewności standardowe oszacowane metodą typu B (wg. B.2, analogicznie jak w przykładzie E.3) są następujące:

V = 2,8 V, u(V) = (0,2 V)/V3 S 0,116 V, 1 = 1,35 mA , u(/) = (0,055 mA)/V3 == 0,0318 mA, natomiast rezystancja wewnętrzna amperomierza r_A = 70 A znana jest z dokładnością 5%, co pozwala na oszacowanie (wg. B.2) niepewności standardowej u(r_A) = (0,05 • 70 fl)/V3 = 2,02 A. (Mierniki analogowe o klasie C = 1% = 0,01)

W zerowym przybliżeniu korzystamy z założenia, że wartość rezystancji możemy wyznaczyć stosując wprost prawo Ohma dla mierzonych wartości:

V    V

R₀=j, natomiast po uwzględnieniu rezystancji amperomierza R = R₀ — r_A= — — r_A

Niepewności oszacowane metodą typu B towarzyszące mierzonym wartościom napięcia i natężenia prądu odzwierciedlają jedynie łączną precyzję odczytu i wskazań przyrządów, toteż nie możemy uznać, że wiążą się ze współzależnymi zmianami natężenia i napięcia, a zatem powinniśmy przyjąć, że niepewności te nie dotyczą istotnie skorelowanych wielkości decydujących o mierzonych wartościach, mimo zależności V = R₀-1. Stosujemy proponowaną w C.l procedurę wyznaczenia złożonej niepewności standardowej dla obliczonej wartości R:

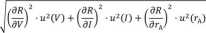
aby po obliczeniu odpowiednich pochodnych cząstkowych i kilku przekształceniach algebraicznych otrzymać:

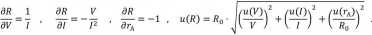
Obliczone wartości: R₀ = 2074,1 fl, a stąd R = R₀ — r_A = 2004 fl z niepewnością standardową u(R) = 98,9 fl (można zauważyć, że niepewność u(r_A) ma znikomy udział w całkowitej niepewności). Wynik pomiaru podajemy (zgodnie z C.3 i D.3) z niepewnością rozszerzoną (dla p = 95% oraz k_p = 2): R = (2,00 ± 0,20) kfl

Odmiennie przebiegałaby analiza i oszacowanie niepewności dla seriii pomiarów w tym samym układzie doświadcza-lym, kiedy wartości mierzonego napięcia i natężenia prądu wykazywałyby znaczący rozrzut wokół wartości przeciętnych. Możliwe byłoby wtedy założenie, że zmienność w mierzonych wartościach jest zwiazana z efektami decydującymi o zmianie np. wartości rezystancji (efekt termiczny podczas przepływu prądu), albo np. fluktuacjami napięcia zasilającego obwód elektryczny - zmienność jednej z tych wielkości decydowałaby np. o zmienności natężenia prądu, a w konsekwencji o zmianach w rejestrowanym napięciu - koniecznym byłoby przeanalizowanie korelacji pomiędzy mierzonymi wielkościami. Procedura oszacowania niepewności pomiaru wymagałaby oszacowania z eksperymentu współczynników korelacji, aby można było posłużyć się algorytmem proponowanym w D.2**.

E.8 Średnia ważona pomiarów tej samej wielkości przy różnych niepewnościach standardowych

Jako przykład rozważmy wyniki pomiaru stałej siatki dyfrakcyjnej otrzymane w różnych warunkach doświadczenia z wykorzystaniem wiązki laserowej: dwa pomiary wykonane dla do pierwszego i drugiego rzędu widma (przy tej samej odległości siatki i ekranu) oraz jeden pomiar w oparciu o pierwszy tylko rząd widma, ale przy znacznie większej odległości siatki od ekranu. Obliczone w oparciu o wyniki pomiarów wartości stałej siatki oraz oszacowane metodą typu B

niepewności standardowe wynoszą:

dj = 4,836 pm	u(dt) = 0,075 pm
d2 = 4,923 pm	u(d2) = 0,039 pm
d3 = 5,043 pm	u(d3) = 0,024 pm

Widoczne jest, że wyniki tych pomiarów mają różną wiarygodność, co odzwierciedla trzykrotnie mniejsza niepewność standardowa dla pomiaru d₃ w porównaniu do pomiaru d₁. Zasadne jest zatem obliczenie średniej ważonej (zgodnie z C.4) zamiast zwykłej średniej arytmetycznej.

Obliczenie niepewności standardowej dla średniej ważonej według procedury C.4 wygląda następująco:

^    /v³    1 \^_1/2 /    1    1    1    \^-1/2

u(d) = (>    -77—    = (—-77 + 7—-77 + 7—-77    = 19,7 nm = 0,020 urn ,

VZ-ii=iU²(tf_i)/ v(75 nm)² (39 nm)² (24 nm)²/

a następnie obliczenie średniej ważonej:

,    V^-13    1    r4,836 lun 4,923 urn 5,043 pmi

“" ^{u W}    - ⁽¹⁹'^7nm)1 -l(75^⁺- ⁴'^9,8'^,m ■

Wynik pomiaru

niepewnością rozszerzoną (dla p = 95%

oraz k_p = 2): d = (4,998 ± 0,039) pm .