3826200343

©msg

Opracowanie wyników pomiarów - oszacowanie niepewności pomiaru

str. 9

E.5 Obliczanie złożonej niepewności standardowej na przykładzie wyznaczania wykładnika adiabaty

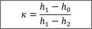
Wartość wykładnika adiabaty dla powietrza wyznaczamy doświadczalnie metodą Clementa Desormes’a w oparciu o pomiary pośrednie oraz będący dobrym przybliżeniem wzór:

Wielkość h₀ jest różnicą poziomów cieczy w rurkach w chwili zamknięcia zaworu, gdy ciśnienie gazu w zbiorniku podczas rozprężania (w przybliżeniu adiabatycznego) wyrównuje się z ciśnieniem otoczenia. Z założenia przyjmujemy w obliczeniach wartość h₀ = 0, jednakże ze względu na wymagany jak najkrótszy czas otwarcia zaworu wielkość ta obarczona jest znaczącą niepewnością, której nie można zaniedbać przy oszacowaniu niepewności standardowej wyznaczanej wartości wykładnika adiabaty. Wartości manometryczne h_lt h₂ odpowiadają zmianie ciśnienia gazu przy rozprężaniu adiabatycznym i ogrzewaniu izochorycznym.

Dysponujemy wynikami pomiarów pośrednich oraz oszacowanymi metodą typu B niepewnościami standardowymi dla tych pomiarów (przykład E.4 - do oszacowania u(h₀) przyjęto A_eh₀ = 4,0 mm ):

| h₀ = 0, u(h_n) = 3,291 mm | h, = 237,0 mm | h₂ = 67.0 mm | u(/i,) = u(h_?) = u(h) = 1,291 mm~| Zgodnie z procedurą C.l obliczamy odpowiednie pochodne cząstkowe dla każdej ze zmiennych, otrzymując:

dic    1    9k    ft₂    9k    h,    ....    ,    ,    „

—— =--: —— = — ———7 : -— = ———r . gdzie dla uproszczenia wykorzystano iuz h₀ = 0 , a na-

dn₀    "i^-«2    otu    lfti^_«2Ż

stępnie wykorzystujemy formułę C.l do obliczenia złożonej niepewności standardowej dla wynikowej wartości k :

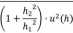
gdzie widać, że wstępne przekształcenia wyrażeń algebraicznych mogą znakomicie ułatwić późniejsze obliczenia.

W oparciu o posiadane wartości liczbowe pomiarów pośrednich i trzech niepewności standardowych oszacowanych metodą typu B oraz wyprowadzony wzór dla złożonej niepewności standardowej wykonujemy obliczenia, przyjmując zgodnie z C.3 współczynnik rozszerzenia k„ — 2 dla poziomu ufności p = 95% oraz zgodnie z D.3 podajemy wynik:

| k = 1,3941    | uQc) = 0,0223 = 0,022    | U(k) = 0,0445 = 0,045    | fc = 1,394 ± 0,045

(*) Do obliczeń wykorzystujemy więcej niż dwie cyfry znaczące niepewności standardowej (wskazówka D.3), aby uniknąć niedoszacowania niepewności rozszerzonej przy mnożeniu przez współczynnik rozszerzenia.

Przy wyznaczaniu tą metodą wykładnika adiabaty nie jesteśmy w stanie oszacować np. efektu systematycznego wynikającego stąd, że proces rozprężania gazu, w warunkach doświadczenia, nie jest ściśle adiabatyczny, co prowadzi do zaniżenia oczekiwanej zmiany ciśnienia w procesie izochorycznym. Efektu tego nie uwzględnia wzór zastosowany do obliczenia wykładnika adiabaty, dając w rezultacie wartość niedoszacowaną. Nie jest to jedyny efekt systematyczny mający wpływ na wynik pomiaru (obecność pary wodnej w powietrzu, zmiana objętości związana ze zmianą poziomu cieczy w manometrze), ale są one znacznie mniej istotne w porównaniu do wspomnianego wcześniej. Należy również pamiętać, że sam wzór będący podstawą do obliczenia wykładnika adiabaty, jest wyprowadzony w oparciu o równanie stanu gazu doskonałego, a nie rzeczywistego.

E.6 Złożenie niepewności typu A oraz typu B dla tej samej wielkości mierzonej

Jest ważne, by nie doprowadzać do podwójnego uwzględniania w obliczeniach tych samych składników niepewności. Jeżeli składnik niepewności wynikający z określonego efektu otrzymano z oszacowania typu B, to powinien on być włączony jako niezależny składnik niepewności przy obliczaniu złożonej niepewności standardowej, ale tylko w takim przypadku, kiedy efekt ten nie wnosi wkładu do obserwowanej zmienności obserwacji (dotyczy C.2). Powodem ograniczenia jest to, że niepewność związana z tą częścią efektów, które wnoszą wkład do rejestrowanej zmienności, jest już zawarta w składniku niepewności otrzymanym z analizy statystycznej wyników obserwacji (metodą typu A).

Jako przykład rozważmy rezultaty oszacowań dla pomiaru czasu spadania kulki metalowej z wysokości h = 50 cm . Włączenie i wyłączenie liczenia czasu przez miernik cyfrowy odbywa się poprzez mechaniczne wyzwalanie przełączników elektrycznych przez spadającą z zadanej wysokości kulkę metalową. Wielokrotnie powtarzany pomiar czasu spadania kulki z tej samej wysokości daje wyniki charakteryzujące się znaczącym rozrzutem. W doświadczeniu wyznaczono (zgodnie z A.l) wartość średnią serii niezależnych odczytów t — 317,3 ms oraz niepewność standardową dla wartości średniej u_A(t) = 1,2 ms. Zakładamy, że niepewność standardowa u_A(t) związana jest jedynie z przyczynami niezależnymi od miernika, a powodującymi rozrzut w wynikach niezależnych pomiarów czasu spadania kulki. Zasadne wydaje się zatem przyjęcie, że wartość średnia z wielu odczytów jest nadal obciążona niepewnością typu B wynikającą z dokładności wskazań przyrządu określonej przez producenta. Dla danego miernika stałe C_t = 3 • 10~³, C₂ = 5 oraz najmniejsza odczytywana wartość Ax_iednos[ta = 0,1 ms, co (zgodnie z B.2) pozwala na oszacowanie niepewności standardowej dla wartości t traktowanej jako odczyt: u_B(t) = (3 • 10^-3 • 317,3 ms + 5 • 0,1 ms)/V3 = 0,84 ms. Zgodnie z C.2 niepewność standardowa pomiaru czasu spadania t = t: u(t) = J (1,2 ms)² + (0,84 ms)² = 1,5 ms