302440164

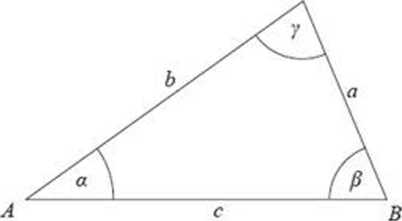
Przyjmujemy oznaczenia w trójkącie ABC: cl b. c

2p=a+b+c

a.ft.y

K K K

R.r

-    długości boków, leżących odpowiednio naprzeciwko wierzchołków A. B. C

-    obwód trójkąta

-    miary kątów przy wierzchołkach A. B.C

-    wysokości opuszczone z wierzchołków A. B. C

-    promienie okręgów opisanego i wpisanego

Twierdzenie sinusów

a

sina sin// siny

= 2 R

Twierdzenie cosinusów

a² -b² + c² - 2/>ccos a h² = a² +C² -2ac cos fi c² = a' +b~ -labcosy

Wzory na pole trójkąta

P. ._Rl- = — ■ a ■ h= — ■ b - h ,= — ■ c ■ h

aABC    a 2    o 2    ^c

P_XABC = —^abs\r\y = —ac-sin// =—bcs'ma

_n _ 1 , sin fi siny _ 1 _u2si na -siny _ 1 ,sina sin//

‘aabc~^u :    t" ¹ 7)    ¹

sina 2 sin fi 2 siny

P = ^rAABC

2 abc 4 R

ABC ^rP

P_s4bc ⁼ 2/?² - sina -sin fi sin y

Lasc = •Jp(p-^(l)(p~^l>)(p-^c)

• Twierdzenie Pitagorasa (wraz z twierdzeniem odwrotnym do niego) W trójkącie ABC kąt y jest prosty wtedy i tylko wtedy, gdy a² + b² = c².

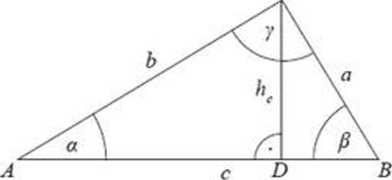
• Związki miarowe w trójkącie prostokątnym

Załóżmy, że kąt y jest prosty. Wówczas: h; =\AD\-\DB\

C

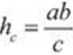
a-c-sina =ccosfi

a-b\ga

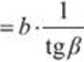
a + b-c 2

p-c

8