3818438321

Zasady zmienności w dynamice układu punktów materialnych i ciała sztywnego.

Środek masy. Momenty bezwładności Pęd i moment pędu. Praca siły i energia kinetyczna.

Zadanie 1

Wyprowadź wzory na główne centralne momenty bezwładności walca kołowego jednorodnego o masie m, promieniu r i wysokości h. Dalej, korzystając z tych wzorów wyznacz główne centralne momenty bezwładności dla jednorodnej cienkiej tarczy kołowej i jednorodnego pręta prostego.

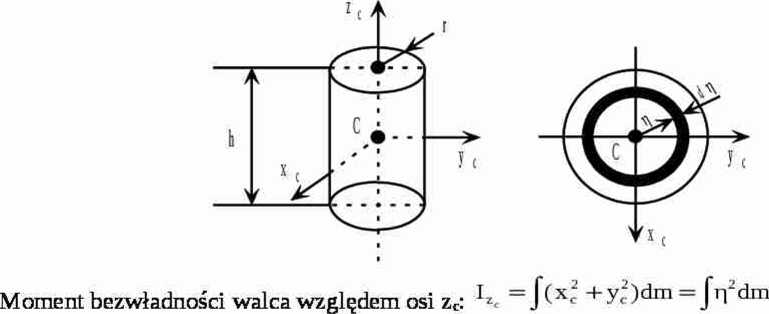
(1)

Masa (m) walca: m = Vp, V = ftĄ, czyli masa elementarna (dm): dm = 27tTjhpdtj i podstawiamy do (1): I*_e =2nhpj^y'dp =2nhp —[p ¹ ]* = —^—, pamiętając, że:m = 7lr²hp,

mr

otrzymujemy: I_z =-

z

^x, ^— ^x_ty_e ^x,z,, dla walca: l_x< Iy_t

wiadomo, że: h_c ⁼ Ix_cz_c + !_Vtz_t, przy czym dla walca: I_XcZ( ^=Iy_cz_t, czyli: h_e = 2I_X(Zt ⁼2Iy_cz_e

I_z    mr■“

4

wobec tego: I_{x z} = I _z = —- =

-JVdm ^ _gdzi_e; d_m = 7Cr²pdz - I_X(V = nr²p fz²dz =Trr²pi[z³] £

m    ^{C C}    J.    3    -

2 1 3

nrph

12

mir

12

pamiętając, że: m = Ttr^hp, otrzymujemy: I_{x v}

wobec tego otrzymujemy: I_x = I_y =

mr² rab² _ m(3r²+ h²)

12

12

mr    mr"

Dla jednorodnej cienkiej tarczy kołowej mamy. h -* 0, czyli: I, =-, I_x =I_V =-

mli²

Dla jednorodnego pręta prostego mamy r -* 0, czyli: I_z. ~0_J y = l_v =

12