7227192432

10. Zbadać okresowość podanych funkcji (jeśli są okresowo to wyznaczyć okres):

/(ar) = 10sin3:r; f(x) = asin A.r + 6cos Xx\ /(rr)\Aan x\ /(rr) = sin²a:, sin \fii.

11. Dane są funkcje: *s(r) = x²; ^/ib(x) ~ 2*. Znaleźć złożenia

oraz ib(ip(x)).

12.    Dana jest funkcja f(x) = j—. Wyznaczyć f(f(f(x))).

13.    Wyrazić f jako funkcję zmiennej x wiedząc, że

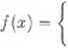
2u. dla u < 0, 0. dla u > 0;.

u =    - 1.

14.    Wiedząc, że f(x - 1) = £² znaleźć J(x + 1).

15.    Znaleźć funkcję odwrotną do funkcji:

io| H

/(i) = 2i + 3; f(r)~x²- 1; /(z) =    log

/M = arcU*3z; /(*) = { £

16.    Podać wzór na $ jako funkcję zmiennej ar jeśli

x² - arecos y =    10^r + 10^y = 10; x-r |y| = 2y.

Znaleźć wykresy podanych funkcji:
2x-Z 10	2x ? 1
^1 3*+ 2’ ^y r^2*fl’	^S'“r> + 1' ^y~" ^ a’
= \fx^\ y = sin z + cos x\	y = cos^2 r; y = r -i- sin zr;
TC	-- 2
y= xsinx\ y — cos-; X	y = =Vsin:r; y = e^x\

V = log(loga;); y =    y = 2 * sin ar; y = [x], y = ar - [ar].