8851785963
Okrąg wpisany i opisany na trójkącie równobocznym
Zad. Oblicz pole pierścienia wyznaczonego przez okrąg wpisany
i opisany na trójkącie równobocznym o polu równym 225V3 cm2.
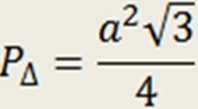
= 225y[3
a2V3 = 900V3
a = 30
aV3 30V3 r_
h = — = —— = 15V3
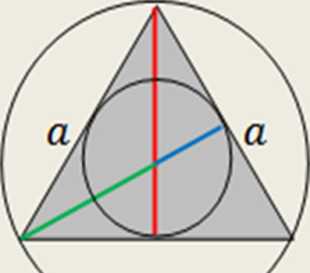
2 2
R=~-h=~- 15V3 = 10V3 r =^ = ^’15V3 = 5V3
Px = nR2 = n ■ (l0V3)2 = 300tt
P2 — ?rr2 = n • (5-y/3) = 75n P1 - P2 = 300tt - 75tt = 2257T
Odp. Pole tego pierścienia wynosi 225n cm
Wyszukiwarka
Podobne podstrony:
Obrazek77 Zadanie 13. (1 pkt) Promień okręgu opisanego na trójkącie równobocznym ma długość —. Pole
Wzor Herona WZÓR HERONA a [ S =7p(p-a)(p-b)(p-c) ] PROMIENIE OKRĘGÓW WPISANEGO I OPISANEGO NA TRÓJK
Dany odcinek o długości 6 jest promieniem R okręgu opisanego na trójkącie równobocznym, zatem wysoko
63 (77) VII WIELOKĄTY I OKRĘGI1 Okrąg opisany na trójkącie 1. Oblicz pole zacieniowanej figury. 3.
Okrąg opisany na trójkącie
Założenie: D średnica okręgu opisanego na trójkącie d średnica okręgu wpisanego w trójkąt G. E.
Elektrotechnika zestaw 1 str 2 Zad. 4. Wyznaczyć rezystancję wypadkową układu przedstawionego na rys
8. Punkt O jest środkiem okręgu opisanego na trójkącie ABC. Punkt K leży na b
56 (100) 56 TRÓJKĄTY PROSTOKĄTNE5 Przekątna kwadratu.Wysokość trójkąta równobocznego 26. Oblicz dług
kolo turbiny 12 1 Zad. 1 Oblicz pole przekroju najmniejszego dyszy Lavala. Ciśnienie pary na wlocie
Pole powierzchni trójkąta Zad. Oblicz pole i wysokość trójkąta o bokach 6cm, 9cm i kącie miądzy tymi
Zad. Oblicz pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnego o krawędzi podstawy
Zdjęcie0112 (5) Zadanie 8: Wyznacz środek okręgu opisanego na trójkącie ABC. CZĘŚĆ ZADANIOWA
IMAG0998 3,5 cm Zadanie 24 e) 120 j on ® 20 y> okręgU opisanego na trójkącie leży ^„kde przecięci
ARKUSZ IX 3 Arkusz IX Zadań e 8. 1 p. Długość promienia okręgu opisanego na trójką
geo1 x X2=? X! Y, Y2=? Zad. 2 Obliczenie współrzędnych punktu Wyznaczyć: współrzędne X2, Y2 punktu 2
ZESTAW 1 q Zad.l Obliczyć pole obszaru, ograniczonego krzywymi y = x3, y2 = x. n Zad.2 Obi. długość
więcej podobnych podstron