1002889891

•    Takie przesunięcie aby prosta 1 pokryła się z osią układu współrzędnych do której jest równoległa, np T(—X₀, — y₀, — Z„) .

•    Obrót o kąt (fi) wokół osi układu współrzędnych na którą 1 została przesunięta.

•    Takie przesunięcie aby prosta 1 znalazła się w postaci wyjściowej

S = T{0,y_o,z_o)*R_x{fi)*T{0,-y_o,-z_ll)

Wykład 6 - Transformacje 3D ciąg dalszy

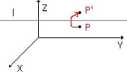
Obrót wokół osi równoległych do osi OX

Pi}/

0

Po-Ho.0)

l^OX

(0,OH™ó(0.0) ^z=<>’-^«iⁿW)+(z-z₀)*^cosW)+z„

si 0X. Znajdujemy macierz

«^^xW=Tlx,,y_a,i_c)*R.Wn-x_l, ,-y„,-z₀)

Oś obrotu przez punkt P₀(x₀, y₀, Z₀) jest równoległa do (fi) we współrzędnych jednorodnych.

	1	H o o	1	0	0
eg,eX(fi) =	0 0	1 0 y0 o 1 Jo	0 0	cos (fi) sin(fi)	—sin(yf) cos(/i)
	0	0 0 1	0	0	0
1 0		0		0
o cos(y?)		-	v„cos [fi)+zc		sin
0 sin (fi)		cos(fi) —	y0sin(fi)-z0cos(fi)+z0
0 0		0		1

0

1

0 1

o o

P' = T(Xn,y„,Zn)*^RAfi)*^lJ(-Xn,-y_l„-zJ*P)=(T(x„,yn,z_a)*R,(fi)*T(-Xn-y₀,-Zn))*P

Obrót wokół osi równoległych do osi OY

Z P-. .

0    0    -x₀

0    -y„

1    Zn

Po^(0,0)

l^OY

obrót

x=(x-x₀)*cos(fi)+(z~z₀)*sm(fi)+x₀

y=y₀

(o,ohp₀(o,o)

z=-(x-x₀)*sm(fi)+(z-z„)*cos{fi)+z_ll

fo. z„)*R,ifl)*T(-x_ll,-y„,-z„)

Oś obrotu przez punkt P₀(x₀, y₀, Z₀) jest równoległa do osi OY. Znajdujemy macierz ^rdmioWei'(/*) ^we współrzędnych jednorodnych.