2659242010

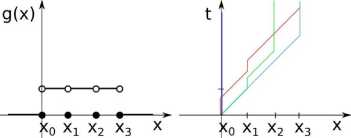
Rysunek 1: Po lewej: Przykładowa prędkość g różnicowania komórek. Punkty Xq,X\,xi,X3 są stanami dyskretnymi, a pozostałe ciągłymi. Po prawej: Wykresy przykładowych trajektorii komórek w przestrzeni stanów odpowiadających tej prędkości różnicowania.

4.2.2    Miarowe warunki przejścia

Miarowe warunki przejścia zostały opracowane w [2] w celu zunifikowanego opisania modelu mieszanego. Wiążą się one z obserwacją, że komórki w stanach dyskretnych (w odróżnieniu od stanów ciągłych) przebywają przez pewien niezerowy czas zanim się zróżnicują. Potrzebna jest dodatkowa relacja mówiąca o tym, ile spośród komórek znajdujących się w danym stanie kwazistacjonarnym, różnicuje się w jednostce czasu. Matematycznie oddaje to równanie:

gi(t)^£r(xt) = ^c,i^t) J_{ <W*)>

gdzie Xi jest punktem kwazistacjonarnym, zaś opisuje gęstość miary fx(t) względem jednowymiarowej miary Lebesgue’a.

4.2.3    Metryka

Ważną kwestią jest stabilność rozwiązań. Mocna topologia w przestrzeni miar nie jest zazwyczaj właściwa dla tego typu zagadnień. Dogodniejszymi okazują się często być słabe metryki. Praca [8] zapoczątkowała ich wykorzystanie w modelach ze strukturą. W wypadku zanurzonego modelu mieszanego wprowadzamy metrykę, która ma własności pośrednie. By ją określić, rozważmy następującą rodzinę funkcji testujących:

^:=

{tp € B{R) : |MU_P < 1, \\ip\_(-oo,_X0]\\Lip < 1, \\tp[(-x₀,xi]\\Li_P < l.---»IIV’L(®j_V__l,x_w]lliip < !}•

Jest to rodzina funkcji borelowskich na R, ograniczonych przez 1 i lipschitzowskich na każdym z przedziałów (a:i_i, a;*] ze stałą Lipschitza ograniczoną przez 1. W punktach Xi jest dopuszczona lewostronna nieciągłość. Miarową metrykę przejścia (ang. measure-transmission metric) definiujemy

8