276061772

fizyka wczoraj, dziś i jutro

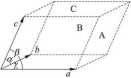
Rys. 7. Schemat opisu parametrów sieciowych w komórce elementarnej

O

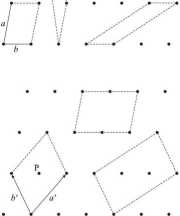
Rys. 6. Niektóre możliwe wybory komórki elementarnej (tu - w sieci płaskiej). Cztery komórki w górnej części rysunku są prymitywne, trzy w dolnej są większe. Zgodnie z podanymi zasadami powinna zostać wybrana komórka prymitywna z opisanymi krawędziami a, b lub centrowana z krawędziami a', b'.

Wspomniane zasady tłumaczą wystarczająco, dlaczego komórka elementarna w układzie heksagonalnym ma w podstawie romb o kącie 120°, a nie sześciokąt (rys. 8). Słup o podstawie sześciokątnej nie jest komórką elementarną, a takie błędne wyobrażenie często można znaleźć w podręcznikach i słownikach³².

Większość kryształów (poza kryształami aperiodycznymi) można opisać, wykorzystując taką trójwymiarową sieć przestrzenną. Sieć przestrzenna może być bowiem traktowana jako pewien trójwymiarowy, geometryczny „szkielet” (schemat) wewnętrznej budowy kryształu³³. Dawniej uważano, że wstawienie w każdy węzeł określonego zespołu elementów fizycznych (atomów lub cząsteczek) zwanego „bazą”³⁴ lub „motywem struktury” pozwoli na „zbudowanie” całego kryształu. Dlatego w pracach fizyków pokutuje pojęcie „sieci krystalicznej”³⁵ na oznaczenie tak rozumianego kryształu.

Dziś wiadomo, że położenie sieci przestrzennej względem „motywu” (lub na odwrót - „motywu” względem sieci) jest całkowicie dowolne. Otrzymamy taką samą sieć, jeśli jej węzeł umieścimy w środku cząsteczki, na dowolnym atomie czy w jakimkolwiek punkcie „motywu”, a więc także poza atomami! Należy pamiętać, że węzły sieci są tylko punktami w przestrzeni i nie wolno ich utożsamiać z atomami tam

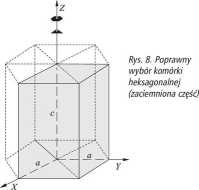
Wydaje się, że nastąpiło tu pomieszanie tzw. symetrycznej prymitywnej komórki Wignera-Seitza o podstawie sześciokątnej z komórką odzwierciedlającą symetrię kryształu.

Jest to twierdzenie słuszne właściwie tylko dla najprostszych struktur; w strukturach bardziej skomplikowanych zbudowanych np. z dużych cząsteczek (por. rys. 9c), trudno od razu dostrzec taką prawidłowość. Nie wolno mylić ze zdefiniowaną wcześniej bazą sieci.

fizyka w szkole