6099520299

2013-01-23

Pozycyjne systemy liczenia (1)

•    Każda liczba całkowita N^2 może być podstawą systemu liczenia (mówimy wówczas o systemie o podstawie N).

•    System dziesiętny (system o podstawie równej 10) używany na co dzień jest przykładem pozycyjnego systemu liczenia

•    System binarny jest także przykładem pozycyjnego systemu liczenia

Pozycyjne systemy liczenia (2)

Do zapisu liczb wykorzystywane są cyfry, których liczba jest taka sama, jak podstawa systemu

—    w systemie dwójkowym: 0,1;

—    w systemie dziesiętnym: 0,1,2,3,4, S, 6,7,8,9;

—    w systemie ósemkowym: 0,1,2,3,4,5, 6,7;

—    w systemie szesnastkowym: 0,1,2, 3,4,5,6,7,8, 9, A, B, C, D, E, F;

—    w systemie o podstawie N: 0,1,N -1

Obliczanie wartości liczby (1)

• system dziesiętny (system o podstawie 10)

353,₁₀₎ = 3 * 100 + 5 * 10 + 3 * 1 = 3 * 10² +

5 * 10¹ + 3 * 10°

2,4₍₁₀₎ = 2*1 + 4* 0,1 = 2* 10°+ 4* 10¹

W = £c • 10'

Obliczanie wartości liczby (2)

System dwójkowy (system o podstawie 2) -Analizowana liczba 101,11,₂₎

lESS""'	_	^1	«	^1
ćyń.	i		,
■Sjjir--					w?

W = £c. . 2’

Interpretacja tej samej liczby w systemie dziesiętnym i w systemie dwójkowym

To, co warto zapamiętać:

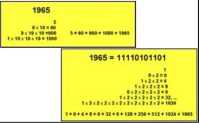
14