614372778

1.4.1 Domknięcie stanu typu e

Pojęcie s-domknięcia jest bardzo istotne w dalszych rozważaniach. Pojęcie to w sposób nieformalny można wprowadzić w następujący sposób: e-domknięcie stanu q to stany które są osiągane tylko i wyłącznie po wszystkich przejściach ze stanu q opatrzonych etykietą e. Inne stany osiągnięte ze stanu q także podlegają tej procedurze, należy przejść do wszystkich e-przejściach.

Formalnie e-domknięcie ED(ą) jest definiowane w następujący sposób:

Podstawa: Stan q należy do ED(<j).

Krok indukcyjny: Jeśli stan p należy do ED(ą) oraz istnieje przejście ze stanu p do stanu r o etykiecie e, to r też należy do ED(ą). Co więcej, dla funkcji przejścia 6 i stanu p € ED(ą) to ED(<j) zawiera także wszystkie stany z 5(p, e).

Dla automatu przedstawionego na rysunku 6 każdy stan jest własnym e-domknięciem oraz dla dwóch stanów mamy: ED(g₀) = {90,9i} oraz EDfe) = {93,95}

Inny przykład, to automat o następującym diagramie:

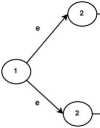
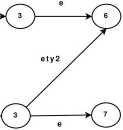
Rysunek 7:

Dla stanu 1 stosując definicję indukcyjną otrzymamy:

ED(1) = {1,2,3,4,6}

1.4.2 Rozszerzona funkcja przejścia

Niech E = {Q, E, 6, qo, F} będzie niedeterministycznym automatem z przejściami e. Funkcja 5 jest rozszerzoną funkcją przejścia, czyli S(q,w) to zbiór stanów osiągalnych po ścieżce, której etykiety tworzą słowo w. Rekuren-cyjna definicja <5 jest określona w następujący sposób:

Podstawa: Wartość rozszerzonej funkcji przejścia jest równa domknięciu, jeśli badaną etykietą dla stanu q jest e: S(q,e) = ED(ą).

Krok indukcyjny: Zakładamy, że w = xa, gdzie a jest ostatnim symbolem w. Ponieważ a należy do E to z definicji nie może ono być równe e. Wartość <5(9, w) może zostać obliczona na trzy sposoby:

1.    Niech 5(q,x) = {pi,p2, • • • -Pk}- Stany pi odzwierciedlają drogę po których możemy dość ze stanu q do stanu x. Ścieżka ta może zawierać e-przejścia, może również kończyć się takim przejściem.

2.    Niech Ui=i ófe,a) = {ri,r2,... ,p_m}- Ten przypadek opisuje drogę, gdzie idziemy po wszystkich przejściach o etykiecie a ze stanów, do których możemy dojść z q po ścieżkach o etykiecie x. Stany Tj to niektóre ze stanów, osiągalne z q po ścieżkach o etykiecie w. Dodatkowe stany, do których możemy dojść, znajdujemy, wychodząc z rj i idąc krawędziami etykietowanymi przez e. Te drogi są opisane w następnym punkcie:

3.    Postać funkcji S(q, w) = Ufci ED(rj) obejmuje domknięcia wszystkich ścieżek z q o etykiecie w. Bowiem, rozważane są możliwości istnienia dodatkowych krawędzi o etykiecie e, które można wykorzystać po dokonaniu przejść na ostatnim symbolu a należącym do E.

Wykorzystując diagram automatu 6 obliczenia wartości 5(qo, 5.6) przedstawiają się następująco:

<5(90, e) = ED(ą₀) = {90,9i}