6581544264

16. Gracz 1, napastnik, strzela karnego graczowi 2, bramkarzowi, i ma do wyboru 2 strategie: strzelać w lewy róg (bramki, widziany od strony boiska) lub w prawy. Bramkarz ma do wyboru 3 strategie: rzucić się w lewy róg (jak wyżej), rzucić się w prawy róg lub zaczekać na to, gdzie strzeli gracz 1. Napastnik na pewno trafi tam gdzie chce i wobec tego na pewno strzeli bramkę, gdy bramkarz rzuci się w przeciwny róg. Jeśli bramkarz od razu rzuci się w ten róg, w który strzela napastnik, obroni karnego z prawdopodobieństwem 0,4 przy strzale w lewy róg, a z prawdopodobieństwem 0,3 przy strzale w prawy róg. Jeżeli zaczeka, obroni strzał w każdy z rogów z prawdopodobieństwem o 0,1 mniejszym, niż gdyby od razu rzucił się w dany róg.

(a)    Podać macierz otrzymanej w tej sytuacji gry o sumie zerowej, w którą wypłatą gracza 1 jest prawdopodobieństwo strzelenia bramki.

(b)    Wyznaczyć wartość tej gry i strategie optymalne obu graczy.

(c)    Czy i ewentualnie jak zmieni się odpowiedź na pytanie (b), gdy gracz 1 ma dodatkowo trzecią strategię strzelania w środek bramki? (Bramkarz na pewno obroni taki strzał, gdy zaczeka, a na pewno nie obroni, gdy rzuci się w któryś z rogów). Uzasadnić odpowiedź.

Roziwązanie

(a) Przy ponumerowaniu strategii:

gracza 1 : 1. L (strzela w lewy), 2. P (strzela w prawy)

gracza 2 : 1. L (rzuca się w lewy), 2. P (rzuca się w prawy) 3. Cz (czeka)

macierzą wypłat gracza 1 jest

(b) Gra oczywiście nie ma równowagi w strategiach czystych, a ponieważ jeden z graczy ma więcej niż 2 strategie, najprostszy algorytm szukania równowag dla gier 2 x 2 nie zadziała. Znajdziemy strategię optymalną gracza 1 - wiemy z teorii, że w grach o sumie zerowej (bądź stałej) jest to strategia równowagi, a więc maksymalizująca (w takich grach) wypłatę gracza 1 przeciw najlepszej odpowiedzi gracza 2. Gracz 1 rozwiązuje więc (przy oznaczeniu x = Xi , 1 — x = Xp) problem

max min(ui((a:, 1 — x), L),ui((:r, 1 — x), P), U\{(x, 1 — x),Cz)) =

*e[o,i]

max min(l — 0,4x, 0,7 + 0,3x, 0,8 — 0, la:) *€[0,1]

Można wyliczyć (a prościej: narysować) te obszary x, w których minimum w nawiasie jest realizowane przez pierwszą, drugą lub trzecią funkcję - czyli strategie bramkarza. Rozwiązaniem jest x = 0,25 ; wówczas

ui(x, P) = ui(x, Cz)

1

[°,25 0,75] -[°’g

0,775,

[0,25 0,75] •

0,7

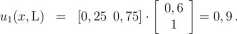
Optymalną strategią napastnika (x) jest więc strzał w lewy róg z prawdopodobieństwem 0,25, a w prawy z prawd. 0,75. Wartość gry wynosi 0,775.