8416073036

kiedy są wykorzystywane do produkcji komputerów, jest a m_h kiedy do produkcji pietruszek. Wyraź ograniczenie na produkcję pietruszek (Q/) i komputerów (Qk) w tej gospodarce. Narysuj je na wykresie Q_P^XQ_K. Ile maksymalnie może ta gospodarka produkować pietruszek, a ile komputerów? (ten punkt jest w pełni analogiczny do zadań z poprzedniego rozdziału).

Teraz dodamy jeszcze jedno ograniczenie: przy produkcji komputerów i pietruszek pracują również ludzie, których w gospodarce jest L. Pracochłonność pietruszek dla ludzi jest Ip, a komputerów dla ludzi wynosi l_K. Wyraź i narysuj to ograniczenie. Ile maksymalnie gospodarka produkowałaby komputerów, gdyby maszyn było wystarczająco dużo? A ile maksymalnie pietruszek?

Narysuj na wykresie Q_P^XQ_K możliwości produkcyjne gospodarki w czterech możliwych sytuacjach: gdy (a) M/m_K > L/l_K i M/m_p > L/lp, (b) M/m_K > L/l_K i M/m_P < L/l_p, (c) M/m_K < L/l_K i M/m_P > L/lp, (d) M/m_K < L/l_K i M/m_P < L/lp.

Kiedy w tych wypadkach będą jakieś niewykorzystane zasoby siły roboczej? Kiedy niewykorzystane zasoby kapitału (czyli maszyn)? (Krugman, Obstfeld, & Melitz, 2012, pp. 82-83).

4.2.    Powiedzmy, że do produkcji pietruszek wykorzystuje się jeszcze ziemię (gdzieś je trzeba uprawiać), której jest Z. Pracochłonność pietruszek dla ziemi jest do produkcji komputerów ziemia jest niepotrzebna. Narysuj możliwości produkcyjne gospodarki dla warunku M/m_K > L/l_K '\ M/ffi_P < L/Ip, kiedy (a) Z/^y < M/mp, (b) Z/^y > L/Ip.

4.3.    Na wykresie Q_P^XQ_K narysuj proste równej wartości \an isoialue linę]. W tym celu zastanów się nad wyrażeniem na sumaryczną wartość V produkcji komputerów i pietruszek w gospodarce, jeżeli cena komputerów to P_K, a pietruszek Pp. Prosta równej wartości to zbiór tych punktów produkcji (czyli koszyków pietruszki^xkomputery), które mają równą wartość pieniężną. Narysuj kilka prostych równej wartości i podaj wzór takiej prostej. Wskaż, które są dla gospodarki lepsze (tj. dla których wartość produkcji jest większa). Od czego będzie zależało nachylenie prostych? Jak na proste wpłynie zmiana ceny pietruszek, a jak komputerów?

Dla trzech różnych nachyleń (bardzo stroma, umiarkowanie stroma, bardzo plaska) pokaż, jaka alokacja ludzi i kapitału będzie najbardziej opłacalna dla gospodarki, w której M/m_K > L/l_K \M/m_p < L/lp. Jakim cenom odpowiadają te nachylenia? (Krugman, Obstfeld, & Melitz, 2012, pp. 83-84).

4.4.    Na wykresie Q_P^XQ_K narysuj krzywą możliwości produkcyjnych:

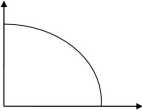
i zinterpretuj jej kształt, odpowiadając na pytania:

(a) pokaż, gdzie, produkując jedną pietruszkę mniej, możemy wyprodukować dużo więcej komputerów;

~11~