8416073117

Przykład:

W poniższym przykładzie szukamy rozwiązania numerycznego układu równań różniczkowych dla równania Eulera dla bryły sztywnej bez sil zewnetrzych:

yl⁼y2^3

y'₃=-0,5l_yiy₂

function dydt = f(t,y) %% zapisujemy równia Eulera dydt = [y(2)*y(3); -y(1)*y(3); -0.51 *y(1)*y(2)];

»tspan = [0 12]; % przedział, dla którego szukamy rozwiązań » yO = [0; 1; 1]; warunki początkowe » ode45(@f,tspan,yO); % metoda ode45

Temat 28

Równania różniczkowe zwyczajne wyższego rzędu

Matlab pozwala również na rozwiązywanie równań różniczkowych wyższego rzędu. W tym przy padku trzeba jednak zapisać równanie w postaci układu równań różniczkowego pierw szego rzędu.

?=f(t,y)

Dowolne równanie różniczkowe wyższego rzędu

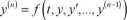
można zapisać jako układ równań pierw szego rzędu stosując podstawienie

y,=y,y₂=y',-,y, =/""¹⁾

Wtedy dostaniemy układ n równani różniczkowych pierwszego rzędu:

y'i=y₂

y'2=y₂

y'n=f{t,yi,yi>-,y_n)

16