8416073538

Przekształćmy obwód wykorzystując twierdzenie Nortona. Schemat do wyznaczania admitancji zespolonej Nortona pokazano na rys. 9.17a., schemat do wyznaczania SPM Nortona na rys. 9.17b, schemat obwodu po przekształceniu na rys. 9.18.

E_,=jlO V

to

lon    5 Q

^al ¹

Olv

(10+jl0)V

Rys. 9.16. Schemat zastępczy obwodu przykładowego IV

10Q    5 Q

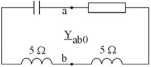
Rys. 9.17a. Schemat do wyznaczania admitancji Nortona

Admitancję zespolona obliczmy jako admitancję dwu gałęzi połączonych równolegle, a więc jako sumę ich admitancji zespolonych.

^Y-N=V-abO=—To7]j ⁺ J7]j ⁼

= j0,2 + (01 - jOJ) = (0,1 + jO,l) S Do wyznaczenia prądu źródłowego Nortona J__N = I__abz wygodnie jest wykorzystać superpozycję (rys. 9.17b.).

E_j= j 10 V

Rys. 9.17b. Schemat do wyznaczania SPM Nortona

Jest:

I>=^a°-=2A 1 r=!°±M₌2A ~ -jl0 + j5    ~    5 + j5

Stąd SPM Nortona ma wartość skuteczną zespoloną:

±N - -abz -L+L Zadany jest przebieg wartości chwilowych

Łn=U*=Ł'+Ł"=4A

napięcia na impedancji Z:

i Iw	> Tab
(0,l+j0,l)S r	Z ^J '

Rys. 9.18. Schemat po przekształceniu

^uz(t)=40 sin(ojI + —) V.    Odpowiada to

wartości    skutecznej    zespolonej:

U_z=40e ⁴ =(20 + j20)V .    Znając    ją

możemy wyznaczyć wartość skuteczną zespoloną prądu I__w.

L_w -(20 + j20) -(0,1 + jO,l) = j4 A Stąd:

Łab=⁴~U=(4~j4)A

Zaś poszukiwana impedancja zespolona ma wartość: