8719220768

METODY PROBABILISTYCZNE I STATYSTYKA - INFORMACJE UZUPEŁNIAJĄCE

1.6. Zadania na ćwiczenia rachunkowe Zadanie 1 - Algorytm sortowania przez wybór⁹

Załóżmy, iż chcemy posortować zbiór liczbowy rosnąco. Zatem element najmniejszy powinien znaleźć się na pierwszej pozycji. Szukamy w zbiorze elementu najmniejszego i wymieniamy go z elementem na pierwszej pozycji. W ten sposób element najmniejszy znajdzie się na swojej docelowej pozycji.

W identyczny sposób postępujemy z resztą elementów należących do zbioru. Znów wyszukujemy element najmniejszy i zamieniamy go z elementem na drugiej pozycji. Otrzymamy dwa posortowane elementy. Procedurę kontynuujemy dla pozostałych elementów dotąd, aż wszystkie będą posortowane.

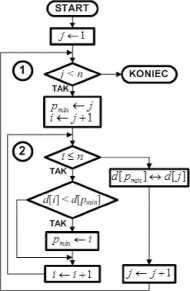
Pętla zewnętrzna sterowana zmienną j wyznacza kolejne elementy zbioru o indeksach od 1 do n -1, w których zostaną umieszczone elementy minimalne. Na początku tej pętli zakładamy, iż elementem minimalnym jest element d[f] i zapamiętujemy jego indeks w zmiennej

W pętli numer 2 sterowanej zmienną i porównujemy pozostałe elementy zbioru z elementem d[p_min\- Jeśli element zbioru d[i\ jest mniejszy od elementu d[p_mj„], to znaleźliśmy nowy element minimalny. W takim przypadku zapamiętujemy jego pozycję w p_mm i kontynuujemy pętlę wewnętrzną.

Po zakończeniu pętli wewnętrznej pmin zawiera indeks elementu minimalnego. Zamieniamy miejscami element d[j] z elementem d[p_mj„]. Dzięki tej operacji element minimalny znajduje się na swojej docelowej pozycji. Zwiększamy j przechodząc do kolejnego elementu zbioru i kontynuujemy pętlę zewnętrzną.

Rysunek 3. Algorytm sortowania przez wybór Dla algorytmu sortowania przez wybór:

1.    Wyznaczyć optymistyczną, pesymistyczną i średnią złożoność obliczeniową.

2.    Wyznaczyć liczbę wykonywanych iteracji dla powyższych przypadków.

3.    Obliczyć wartości powyższych wskaźników dla n = 10.

4.    Porównać obliczone wartości z wynikami symulacji¹⁰ liczby porównań w której dla n = 10 dla wszystkich sprawdzanych danych otrzymano taką samą liczbę porównań, równą 55.

5.    Dla otrzymanych wyników symulacji ocenić korelację pomiędzy liczbą porównań - L i liczbą sortowanych, przypadkowo ustawionych danych - N:

L	55	78	105	136	171	210	253	300	351	406
N	10	12	14	16	18	20	22	24	26	28

⁹    http://edu.i-lo.tarnow.pl/inf/alg/003 sort/0009.php

¹⁰    http://www.home.umk.p1/~abak/wdimat/s/SelectSort.html

14

Data ostatniej aktualizacji: piątek, 29 października 2010