8719220773

METODY PROBABILISTYCZNE I STATYSTYKA - INFORMACJE UZUPEŁNIAJĄCE

System jest efektywny, jeśli zadowalająco wykonuje powierzone zadania w dłuższym okresie czasu.

Analizując dokładniej efektywność z punktu widzenia czasu, dochodzimy do wniosku, że pojęcie to ma tak wielkie znaczenie, jak pojęcia niezawodności i możliwości konserwacji.

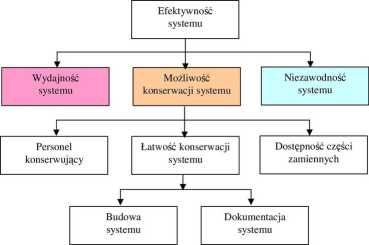
Rysunek 7. Związki miedzy wydajnością, możliwością konserwacji oraz niezawodnością systemu

Możliwość konserwacji systemu jest to prawdopodobieństwo tego, że w określonym przedziale czasowym po wystąpieniu uszkodzenia (błędu) można doprowadzić system do pełnych możliwości funkcjonalnych. Średni czas potrzebny do usunięcia błędu lub usterki nazywa się średnim czasem naprawy t_n (ang. mean time to repair - MTTR). Ten interwał czasowy rozpoczyna się w chwili powstania niesprawności i kończy z ponownym przywróceniem działania systemu. Możliwość konserwacji jest zależna od pewnej liczby czynników: możliwości dysponowania personelem konserwującym, umiejętności tego personelu, dostępności części zamiennych oraz łatwości konserwacji systemu.

Łatwość konserwacji jest prawdopodobieństwem, że błędnie działający system może być zreperowany w określonym przedziale czasowym przez przeciętny personel konserwujący, przy założeniu dostępności wszystkich potrzebnych części zamiennych. Ponieważ możliwość konserwacji w każdym konkretnym przypadku zależy od organizacji prac konserwacyjnych, łatwość konserwacji stanowi charakterystykę systemu, zależną od jego budowy, dokumentacji itd.

Dla praktycznych zastosowań duże znaczenie ma średni czas między uszkodzeniami t_mu (ang. mean time between failures - MTBF). Pojęcie to można wprowadzić, gdy zachowanie się błędów systemu nie zmienia się przez dłuższy czas w porównaniu ze średnim czasem między uszkodzeniami. Mówi się wówczas o stałej intensywności pojawiania się błędów albo, inaczej, o stałym prawdopodobieństwie niesprawności na jednostkę czasu. Zakłada się przy tym, że system działa poprawnie na początku rozważanego przedziału czasowego. Średni czas między uszkodzeniami t_mu jest sumą średniego czasu do kolejnego uszkodzenia tk_U (ang. mean time to fail - MTTF) oraz średniego czasu naprawy t_n

tmu = tku + tn

19

Data ostatniej aktualizacji: piątek, 29 października 2010