8719220779

METODY PROBABILISTYCZNE I STATYSTYKA - INFORMACJE UZUPEŁNIAJĄCE

4)    wybiera się następny element (14), i porównuje z elementami listy - ponieważ dopiero dla ostatniego elementu 14 < 16, to liczby z pozycji trzeciej i czwartej przesuwa się odpowiednio na pozycję drugą i trzecią, a na zwolnioną pozycję czwartą wstawią się liczbę 14. Zatem 12 I 11 13 14 16

5)    wybiera się ostatni (12), i porównuje z elementami listy. Dla trzeciej pozycji 12 < 13, to liczbę 11 z pozycji drugiej przesuwa się na pozycję pierwszą, a na zwolnioną pozycję wstawią liczbę 12. Zatem 111 12 13 14 16

W tabeli 1 podano schemat blokowy algorytmu, opis w pseudokodzie, liczbę wykonań poszczególnych instrukcji i komentarz.

Zakładając, że czas wykonania każdej instrukcji wynosi c*, na podstawie tabeli 1 można podać wzór na złożoność czasową.

Z,(n) = c ,+nc₂+(n-1 )c₃+(n-1 )c₄+    t(i) c₅+( £ t(i) -1 )c₆+( £ Ki) -1 )c₇+(n-1 )c₈+(n-1 )c₉

Po uporządkowaniu otrzymujemy zależność w postaci następującej:

Zi(n) =(Ci-C₃-C4-C6-C₇-C₈-C9) + (C₂+C3+C4+C₈+C₉)n + (c₅+c₆+c₇) 2 t(i)

Wprowadzając oznaczenia: d i =c i -C3-C4-C6-C7-C8-C9

d2=C2+C3+C4+C8+C9

d₃=C5+C6+C₇

otrzymuje się ostateczny wzór na złożoność czasową algorytmu / programu na sortowanie przez wstawianie

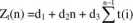
Ocena optymistyczna

Tablica jest już posortowana na samym początku - a zatem wykonanie algorytmu jest zbędne. Wszystkie elementy są na właściwych miejscach, a więc liczba sprawdzeń tj będzie równa 1 przy każdym obrocie zewnętrznej pętli. Wówczas funkcja złożoności jest następująca:

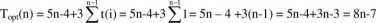
Otrzymaliśmy liniową zależność od n!

Ocena pesymistyczna

W tym przypadku podana tablica jest także posortowana, ale... w odwrotnym porządku! Wtedy też wszystkie elementy muszą być kolejno posyłane na koniec tablicy: i-ty element przemieści się więc o i - 1 miejsc do tyłu w każdym obrocie zewnętrznej pętli. Wniosek: t, = i dla każdego i = 2, 3, ..., n. Funkcja T(n) będzie zatem wyglądała tak:

Tpe,(n) = 5n-4+3£i

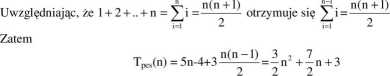
-n =

Otrzymaliśmy więc funkcję kwadratową.

n(n-l)

2

Data ostatniej aktualizacji: piątek, 29 października 2010

6