8955898800

216

i

Rys. 5.8.45. Wynik optymalizacji wartości wymiarów metodą analizy wariantowej (I-DEAS) Fig. 5.8.45. The resulł of optimizing of dimensions valucs using the method of vanants analysis (1-DEAS)

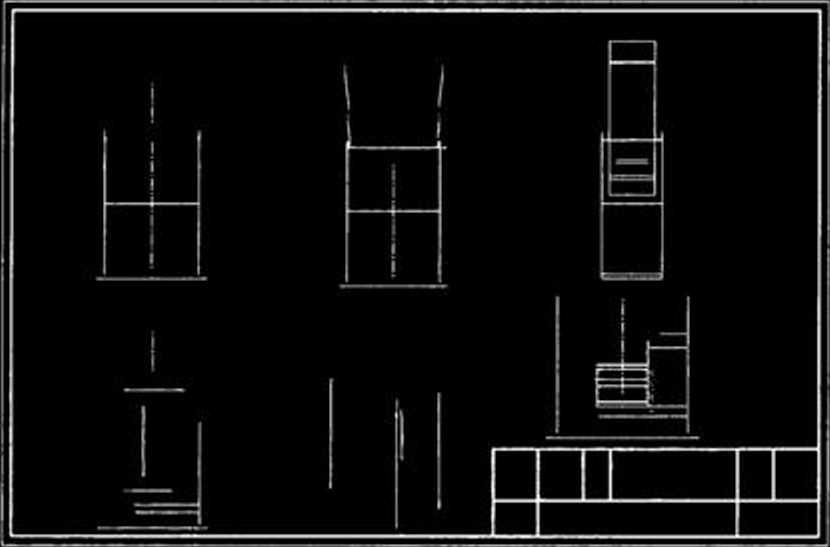
I-DEAS

Fig. 5.8.46. Transformation of notation of a 3D constniction in the graphic program I-DEAS

5.9. Reguły doboru konstrukcji uporządkowanych

Reguły doboru w uporządkowanych rodzinach konstrukcji RG_n wyznaczają relacje między zapotrzebowaniem, określonym przez ilościowe i jakościowe cechy charakterystyczne CCH. a uporządkowanymi konstrukcjami rodziny konstrukcji RK \ Modele tworzenia reguł doboru przedstawiono również w pracach [21,129).

Niezależnie od przeznaczenia uporządkowanej konstrukcji, czy to dla: wytworzenia nowego środka technicznego lub zastosowania w bardziej złożonej konstrukcji, jej wybór przeprowadza się na podstawie wymaganych cech charakterystycznych CCH*, identyfikowanych przez wektor potrzeb X. oraz dodatkowe wymagania DW„ [21]. Zasada wyboru wektora potrzeb X.’ polega na wyborze takich wartości uporządkowanych cech charakterystycznych, które są najbliższe większe od wartości cech wymaganych (jdeh gradient wymagań jest dodatni, tzn. wzrost wartości cech charakterystycznych jest związany ze wzrostem wartości ilościowych cech konstrukcyjnych)

x* = N‘(x„).    (5.144)

Powyższa zasada wyboru pojawia się wówczas, gdy w uporządkowanej rodzinie konstrukcji występuje przyporządkowanie dyskretne (rozdz. 4). W przypadku przyporządkowania ciągłego położenie wymaganego wektora potrzeb decyduje o wyborze obszaru uporządkowanych potrzeb OP, (rys. 4.1). Po określeniu zunifikowanego wektora potrzeb X" lub obszaru potrzeb OP, przystępuje się do wyboru uporządkowanej konstrukcji na podstawie reguł doboru RG„.

Reguły doboru RG, tworzone są na podstawie przyporządkowania: a, P, x. 8

RG_B^K=f(a,p,x.8).    (5.145)

Występuje we wszystkich uporządkowanych rodzinach konstrukcji z różnym stopniem złożoności. Najbardziej złożone są reguły doboru w systemach modułowych konstrukcji, których model przedstawiono na rys. 5.9.la. Wektorowi potrzeb X’ oraz dodatkowym kryteriom i wymaganiom DW,,, przyporządkowana jest droga grafu wariantów konstrukcyjnych pftks^.tks^). Wynikiem przyporządkowania a jest typowa postać

konstrukcyjna środka technicznego rV'. Uwzględniając dodatkowo układ wymiarów rysunku złożeniowego W¹’, tworzy się konstrukcję modułową Ks*

(X\DW.)—i-♦^^,'{^(tks^tks^))uW^,•    =Ks;.    (5.146)

Wybranym typowym rozwiązaniom konstrukcyjnym    (tks/.tks^) na podstawie

przyporządkowania P, odpowiadają typowe postacie konstrukcyjne elementów n"’

(tks;¹,tks^)—*-♦ |J(n,;(j-    jz)>-    (5.147)

Zapis typowej postaci konstrukcyjne n"’ wraz z układem wymiarów UW"’ tworzy rysunek wykonawczy z otwartym układem wymiarów ZK"' (rozdz. 5.6, rys. 5.6.2).